Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.1 - Ex. 22
Ache o volume do sólido gerado pela rotação da região limitada pela curva , pelo eixo , e pelas retas e em torno do eixo .
Passo 1
Para entendermos como é a região e qual vai ser a integral, vamos olhar um esboço dela:
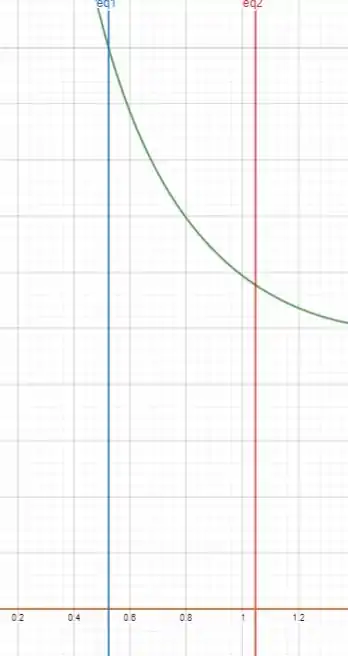
A região é entre a curva verde e a laranja, limitadas pelas retas azul e vermelha
Entao teremos, até . Onde o raio do disco vai ser a própria função verde:
O volume vai ser:
Passo 2
Vamos resolver essa integral:
Primeiro, vamos ver a integral indefinida:
Passo 3
Voltando para a nossa integral definida:
Lembrando que
Vamos ter:
Dessa forma:
Resposta
Exercícios de Livros Relacionados
Ache o volume do sólido gerado pela rotação de um arco da senóide em torno do eixo x .
Ache o volume do solido gerado por rotação, em torno do eixo x da região limitada pela curva y = s e n x , a reta x= 1 2 π e eixo x.
Ache o volume do solido gerado por rotação, em torno do eixo y da região limitada pela curva x = y ² ² e x = y 4 , no primeiro quadrante
Ache o volume do solido gerado por rotação, em torno do eixo x da região limitada pela curva y = x c o s e c x , a reta x= 1 2 π , x= 1 4 π e eixo x.
Ache o volume do solido gerado por rotação, em torno do eixo y da região limitada pela curva x = c o s y , a reta y = 1 6 π e eixo y