Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.1 - Ex. 24

A região limitada pelo eixo y e pelas curvas y = sen ⁡ x e y = cos ⁡ x para 0 ≤ x ≤ π 4 é girada em torno do eixo x . Ache o volume do sólido gerado.

Passo 1

Para entendermos como é a região e qual vai ser a integral, vamos olhar um esboço dela:

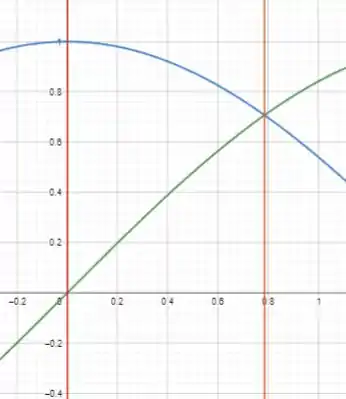
A região é entre a curva verde e a azul. Limitada por aquela reta vermelha. O intervalo começa em x = 0 , e termina em x = π 4 .

Mas vamos verificar que de fato as curvas se encontram em π 4

sen ⁡ x = cos ⁡ x → tg ⁡ x = 1 → x = π 4

Beleza, é ali mesmo onde elas se cruzam.

Na verdade aqui, temos duas regiões. Uma do cosseno, em azul, até o eixo x e uma do seno, em verde, até o eixo x .

O volume vai ser a subtração dessas duas:

V = V 1 - V 2

Onde:

Cosseno → V 1

seno → V 2

Vamos ver os raios de cada região:

r 1 x = cos ⁡ x

Da vermelha para a verde, vamos ter:

r 2 x = sen ⁡ x

O volume vai ser a subtração dos dois volumes,

V = V 1 - V 2

V 2 = ∫ 0 π 4 π sen ⁡ x 2 d x = ∫ 0 π 4 π sen 2 ⁡ x d x

V 1 = ∫ 0 π 4 π cos ⁡ x 2 d x = ∫ 0 π 4 π cos 2 ⁡ x d x

Passo 2

Vamos resolver essas integral:

V 2 = ∫ 0 π 4 π sen 2 ⁡ x d x

V 2 = π ∫ 0 π 4 sen 2 ⁡ x d x

Primeiro, vamos ver a integral indefinida:

∫ sen 2 ⁡ x d x

Para isso, vamos usar que:

sen 2 ⁡ x = 1 - cos ⁡ 2 x 2

Colocando essa expressão na integral:

∫ 1 - cos ⁡ 2 x 2 d x = ∫ 1 2 - cos ⁡ 2 x 2 d x = x 2 - sen ⁡ 2 x 4 + C

Passo 3

Voltando para a nossa integral definida:

V 2 = π ∫ 0 π 4 sen 2 ⁡ x d x = π x 2 - sen ⁡ 2 x 4 0 π 4 =

π π 8 - sen ⁡ π 2 4 - π 0 2 - sen ⁡ 0 4 =

π 2 8 - π 4

Passo 4

Agora a outra

V 1 = ∫ 0 π 4 π cos 2 ⁡ x d x

V 1 = π ∫ 0 π 4 cos 2 ⁡ x d x

Primeiro, vamos ver a integral indefinida:

∫ cos 2 ⁡ x d x

Para isso, vamos usar que:

cos 2 ⁡ x = 1 + cos ⁡ 2 x 2

Colocando essa expressão na integral:

∫ 1 + cos ⁡ 2 x 2 d x = ∫ 1 2 + cos ⁡ 2 x 2 d x = x 2 + sen ⁡ 2 x 4 + C

Passo 5

Voltando para a nossa integral definida:

V 1 = π ∫ 0 π 4 cos 2 ⁡ x d x = π x 2 + sen ⁡ 2 x 4 0 π 4 =

π π 8 + sen ⁡ π 2 4 - π 0 2 + sen ⁡ 0 4 =

π 2 8 + π 4

Passo 6

Nosso volume vai ficar:

V = V 1 - V 2 = π 2 8 + π 4 - π 2 8 - π 4 = π 4 + π 4 = π 2

Resposta

π 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo y x = y 3 2 x = 0 y = 2
Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo y x = cos ⁡ π y 4 - 2 ≤ y ≤ 0 x = 0
Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo y x = 2 y + 1 x = 0 y = 0 y = 3
Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo y x = 2 y y 2 + 1 x = 0 y = 1
Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo x y = sec ⁡ x y = 2 - π 4 ≤ x ≤ π 4