Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.3 - Ex. 39

Ache o volume do sólido gerado pela rotação da região limitada pela curva y = sec 2 ⁡ x , pelos eixo𝑠 e pelas reta x = 1 4 π em torno do eixo x .

Passo 1

Primeiramente vamos montar o gráfico das funções e a região hachurada que é por onde vamos calcular o volume do sólido.

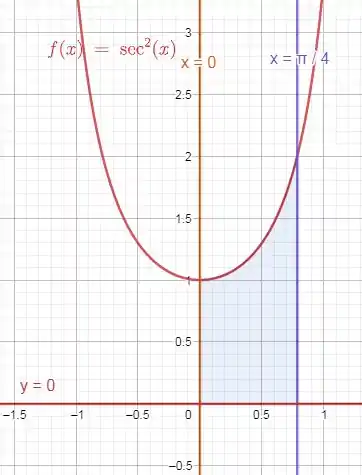
Passo 2

Agora vamos montar a integral do sólido usando a fórmula π ∫ a b f ( x ) 2 d x . O limite de integração vai de 0 a 1 4 π e f x = sec 2 ⁡ x .

π ∫ 0   1 4 π   sec 2 ⁡ x 2 d x

π ∫ 0   1 4 π   sec 4 ⁡ x d x

Passo 3

Agora vamos resolver a integral usando a seguinte fórmula ∫ sec n ⁡ x d x = sin ⁡ x sec n - 1 ⁡ x n - 1 + n - 2 n - 1 ∫ sec n - 2 ⁡ x d x .

π ∫ 0   1 4 π   sec 4 ⁡ x d x = π sin ⁡ x sec 3 ⁡ x 3 0 1 4 π + 2 3 ∫ 0   1 4 π   sec 2 ⁡ x d x

π sin ⁡ x sec 3 ⁡ x 3 + 2 3 tan ⁡ x 0 1 4 π

π sin ⁡ 1 4 π sec 3 ⁡ 1 4 π 3 + 2 3 tan ⁡ 1 4 π - sin ⁡ 0 sec 3 ⁡ 0 3 + 2 3 tan ⁡ 0

π 2 3 + 2 3 - 0

4 3 π

Resposta

4 3 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

48. Dois cilindros circulares retos, cada um tendo um raio de r unidades, têm seus eixos interceptando-se em ângulos retos. Ache o volume do sólido comum aos dois cilindros.
46. Resolva o Exercício 46, se os triângulos retângulos isósceles tiverem um dos catetos no plano da base.
50. Uma cunha é cortada de um sólido com a forma de um cone circular reto e tendo um raio de base com 5cm e uma altura de 20cm, por dois planos contendo o eixo do cone. O ângulo entre os planos tem um
49. Uma cunha é cortada e um sólido com a forma e um cilindro circular reto, o qual tem um raio de r cm, por um plano através de um diâmetro da base e inclinado em relação ao plano da base segundo um
Demonstre o volume de um tronco de cone circular reto