Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 6.3 - Ex. 37

A região limitada pelas curvas dadas é girada ao redor dos eixos especificados. Ache o volume do solido resultante por qualquer método

y = x 2 + x - 2 , y = 0 ; ao redor do eixo x

Passo 1

Inicialmente, vamos analisar o gráfico de nossa x 2 + x - 2 . Então vamos achar as raízes.

x 2 + x - 2 = 0

Logo,

x = - 1 ± 1 - 4 ⋅ 1 ⋅ - 2 2 → x = - 2   o u   x = 1

Então o gráfico fica o seguinte:

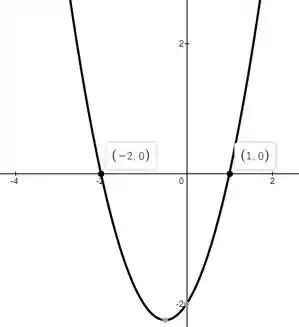
Nessa questão vamos usar o método dos discos. Vem comigo!

V = ∫ a b π f x 2 d x

Logo,

V = ∫ - 2 1 π x 2 + x - 2 2 d x

Abrindo esse termo ao quadrado:

x 2 + x - 2 2 = x 2 + x 2 - 4 x 2 + x + 4

Isto é,

x 2 + x - 2 2 = x 4 + 2 x 3 - 3 x 2 - 4 x + 4

V = ∫ - 2 1 π x 4 + 2 x 3 - 3 x 2 - 4 x + 4 d x

Não esquece: ∫ x n d x   = x n + 1 n + 1 + c   quando   n   ≠ - 1

Passo 2

Integrando, temos:

V = π x 5 5 + 2 x 4 4 - 3 x 3 3 - 4 x 2 2 + 4 x - 2 1

Aplicando entre esses pontos:

V = π 1 5 + 2 4 - 3 3 - 4 2 + 4 - 2 5 5 + 2 ⋅ 2 4 4 - 3 ⋅ 2 3 3 - 4 ⋅ 2 2 2 + 4 ⋅ 2

Fazendo as contas:

V = 81 π 10

Resposta

V = 81 π 10

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um buraco com 2 3 cm de raio é feito através do centro de um sólido esférico com 4 cm de raio. Ache o volume da parte do sólido que foi cortada fora.
Ache o volume do sólido gerado pela rotação da região no primeiro quadrante limitada pela curva y = c o s ( x 2 ) e pelos eixos coordenados em torno do eixo y.
A região no primeiro quadrante, limitada pela curva x = c o s y 2 , pelo eixo y, e pelo eixo x, onde 0 ≤ x ≤ 1 gira em torno do eixo x. Ache o volume do sólido gerado.
Um buraco com 2 cm de raio é feito através de um sólido esférico de 6 cm de raio e o eixo do buraco é um diâmetro da esfera. Ache o volume da parte que sobra da esfera.
Ache o volume do sólido gerado pela rotação da região limitada pela curva x 2 3+y 2 3 = a 2 3 em torno do eixo y.