Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.Revisão - Ex. 2

Ache o volume do solido gerado por rotação, em torno do eixo y da região limitada pela curva y = x 4 , a reta x= 1 e eixo x

Passo 1

Oiii, temos que calcular um volume de um solido de revolução. Vamos primeiro ver com que região estamos trabalhando

y   =   x 4

x =   1  

  e i x o   x      

Podemos também escrever esses limites como

y   =   x 4

x =   1  

y = 0

Afinal o eixo x é a reta y = 0 . Podemos ver essa região abaixo

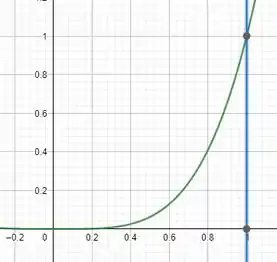
A curva verde a função y =   x 4 e a azul x = 1   .   Como é um solido de revolução. Então podemos usar a seguinte formula para calcular seu volume

∫ a b π f x 2 d x

Passo 2

Como agora o eixo de rotação é y, nossa função tem que ser em função de y. Então podemos dizer que nossa fórmula genérica fica

∫ a b π f x 2 d x → ∫ c d π f y 2 d y

Belezinha? Se pegarmos nossos dados do enunciado nossa integração fica da seguinte maneira

∫ c d π 1   –   y 1 / 4   2 d x

No nosso caso o limite de integração em y é no intervalo [1,0], como podemos ver no gráfico. Ah aliás, essa é uma boa dica. Faça Os gráficos das regiões. Isso sempre ajuda a encontrar os limites e se orientar. Beleza! vamos continuar. Dessa forma nossa integração fica

V   =   ∫ 0 1 π 1   –   y 1 4 2 d y            

= π ∫ 0 1 1 2 - 2 y 1 4 + y 1 2 d y            

= π ∫ 0 1 1 d y - ∫ 0 1 2 y 1 4 d y + ∫ 0 1 y 1 2 d y

=   π y - 2 . 4 5 y 5 4 + 2 3 y 3 2   0 1  

=   π 1 - 8 5 + 2 3

=   π 15

Terminamos por aqui. Pode comemorar! \o/

Te vejo na próxima resolução

: )

Resposta

V = π 15

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 27 e 28, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados. 28 – C – Para a reta y = 5 .
Nos Exercícios 27 e 28, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados. 27 – B – A reta y = 1.
Nos Exercícios 27 e 28, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados. 28 – D – Para a reta y = - 5 8 .
Nos Exercícios 27 e 28, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados. 27 – A – O eixo x.
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.26 - y = x 4ey = 4 - 3 x 2 A