Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.Revisão - Ex. 7

7. Ache do volume do sólido gerado pela rotação em torno do eixo y da região limitada pela parábola x = y 2 + 2 e pela reta x = y + 8 .

Passo 1

Primeiro temos que achar a região limitada pelas funções dadas. Devemos encontrar os pontos de integração.

Para isso igualamos: y ² + 2 = y + 8             →             y ² - y - 6 = 0

Encontrando as raízes: y 1 =     1 + 1 2 - 4.1 - 6 2.1 =   1 + 5 2 = 6 2 = 3

y 2 =   1 - 25 2 =   1 - 5 2 =   - 2

Passo 2

Observe a figura 1 vemos a região pedida.

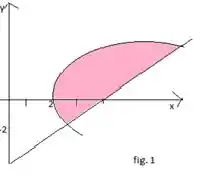
Basta encontrar as intersecções, pois será os intervalos de integração basta fazer que;

V =   π ∫ - 2 3 y + 8 2 - y 2 + 2 2 d y

V = π ∫ - 2 3 - y 4 - 3 y 2 + 16 y + 60 d y

V =   π   ( - y 5 5 - y 3 + 8 y 2 + 60 y ) | 3 - 2 Aplicando os intervalos temos;

V =   π . 250

V = 250 π

Resposta

V = 250 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Escreva, mas não calcule, uma integral para o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno da reta especificada. y = c o sx ,y = 2 - cos ⁡ x ,0 ≤ x ≤ 2 π ; e mt
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta dada. R 3e mt o r n od eO A
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta dada. R 2e mt o r n od eB C
Escreva, mas não calcule, uma integral para o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno da reta especificada. y = 0 ,y = s e nx ,0 ≤ x ≤ π ; e mt o r n od ey
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta dada. R 3e mt o r n od eO C