Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.3 - Ex. 7
(a)Complete a tabela e dê um palpite sobre o limite indicado.
,
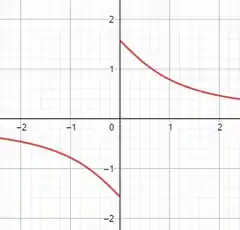
(b)Use a Figura 1.3.3 para encontrar o valor exato do limite na parte (a).
Passo 1
(a)Completando a tabela com o auxílio de uma calculadora científica, teremos:
Conseguimos notar que, quanto menor o valor de usado pra calcular , mais se aproxima de .
Passo 2
(b)Esse não é um limite que pode ser calculado diretamente. Pelo gráfico da função, observamos que, ao se aproximar de 0 pela direita, a função tende a um número próximo de 2.
Esse valor é aproximadamente 1,57, que equivale, também aproximadamente, a . E equivale a em radianos. Assim, comprovamos pela tabela que:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
51-56. Use as Definições 1.4.2 ou 1.4.3 para provar que o limite dado está correto.54. lim x → - ∞ x x + 1 = 1
59-64. Use as Definições 1.4.4 ou 1.4.5 para provar que o limite dado está correto.59. lim x → 3 1 x - 3 2 = + ∞
42. a) Encontre os valores de x 1 e x 2 na figura abaixo.b) Encontre um número positivo N , tal que: 1 x 3 - 0 = 1 x 3ϵ Com xN .c) Encontre um número negativo N , tal que: 1 x 3 - 0 = 1 x 3ϵ Com xN .
51-56. Use as Definições 1.4.2 ou 1.4.3 para provar que o limite dado está correto.56. lim x → - ∞ 2 x = 0
59-64. Use as Definições 1.4.4 ou 1.4.5 para provar que o limite dado está correto.62. lim x → 1 1 x - 1 = + ∞