A água, descendo por um trecho reto de um rio, em geral escoa mais rapidamente no meio e a velocidade escalar diminui para quase zero nas margens. Considere um trecho longo de rio escoando para o norte com as margens paralelas distando 40 m uma da outra. Se a velocidade escalar máxima da água é de 3 m/s, podemos usar uma função quadrática como modelo básico para encontra a taxa com que escoa água unidades de distância da margem oeste:
a) Um barco se move com uma velocidade escalar constante de 5 m/s a partir de um ponto A na margem oeste enquanto se mantém direcionado perpendicularmente à margem. A que distância rio abaixo, na margem oposta, o barco vai atingir a terra firme? Faça um gráfico para a trajetória do barco.
b) Suponha que quiséssemos pilotar o barco a fim de atracar em ponto B, diretamente oposto ao A, na margem leste. Se mantivermos a velocidade escalar constante de 5 m/s e uma direção constante, determine o ângulo no qual o barco deve ser conduzido. Depois, faça o gráfico do caminho real que o barco segue. Essa trajetória parece realista?
Passo 1
Olá, meu amigo. Vou te ajudar a resolver essa redação em forma de questão.
No ensino médio você já deve ter visto esse tipo de questão, a única diferença é que lá a velocidade da correnteza do rio era constante, aqui ela não é!
Vamos visualizar a nossa situação:
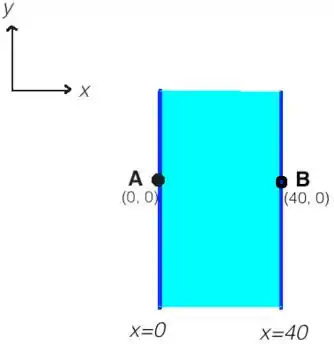
Na modelagem do problema, precisamos definir algumas coisas:
- vamos começar colocando a direção sul-norte no eixo (que aponta para o norte) e a direção oeste-leste no eixo (apontando para leste).
- Além disso, vamos colocar o ponto de partida A como sendo a origem do sistema de coordenadas. Daí basta escrever as componentes do vetor velocidade em cada caso e integrar para achar a posição.
É importante lembrar que a função nos dá a velocidade da correnteza do rio que aponta na direção do eixo .
Para a letra a), queremos saber a que distancia rio abaixo, isso é, sua distância em , ele vai ter parado? Iremos utilizar dos nossos conhecimentos em relação a integral para dada a equação da velocidade em , descobrirmos a equação do espaço em .
Fazermos isso integrando a equação da velocidade.
Para a letra b), queremos saber qual o ângulo de inclinação deveremos conduzir nosso barco para compensar o fato de que a velocidade da correnteza não nos deixará nos deslocarmos em linha reta, sendo assim precisaremos compensar isso de alguma forma, então deveremos inclinar em relação a horizontal.
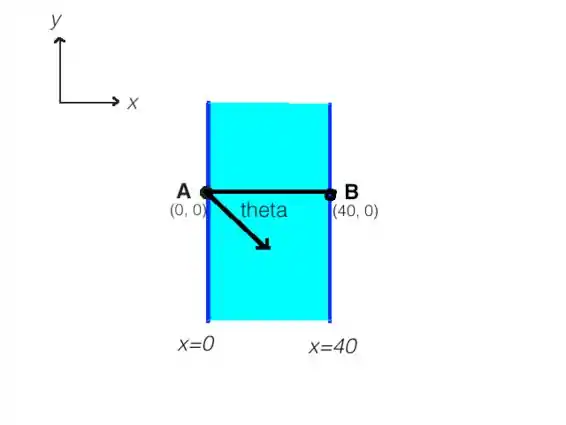
Passo 2
Neste passo vamos resolver o item (a).
Bom, neste caso, a velocidade do barco será constante igual a 5 m/s e na direção , de modo que
Já para a correnteza, teremos
Desta forma,
Assim, podemos escrever
Da primeira equação, tiramos que . Como em , temos , segue que . Assim, . Substituindo isso na segunda equação:
Portanto,
Integrando essa equação e usando que , obtemos que
Temos então que a trajetória, parametrizada pelo tempo, é:
O barco atinge a outra margem quando , de modo que
Assim, a coordenada será
O barco atingirá a margem oposta a uma distância de rio abaixo. O gráfico da trajetória do barco é mostrado a seguir:
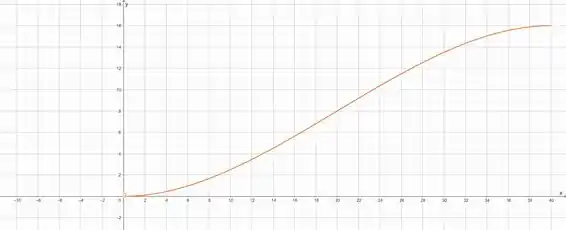
Veja que temos a relação aqui do deslocamento em versus o deslocamento em até
Passo 3
Neste passo vamos resolver o item (b):
Nesta situação, a velocidade do barco não estará na direção . Se for o ângulo que o barco faz com a direção (o mesmo ângulo das coordenadas polares) e este ângulo for constante, a velocidade do barco com relação ao rio será
Assim,
Desta forma,
Integrando a primeira equação e usando que , obtemos
Substituindo isso na segunda equação, temos que
Integrando com relação ao tempo e usando que para , :
Assim,
O barco atinge a margem oposta quando , assim
Substituindo isso na equação para , temos que
Queremos que o barco atinja a margem oposta sem se deslocar na direção do rio, de modo que . Assim, temos que
Portanto,
A trajetória do barco é:
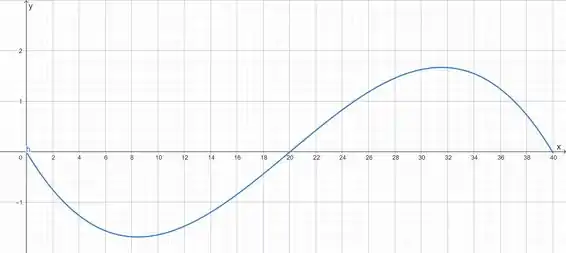
Veja que temos a relação aqui do deslocamento em versus o deslocamento em até
Resposta
.
b) .