Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.4 - Ex. 43
O módulo do vetor aceleração é . Use a figura para estimar as componentes tangencial e normal de .
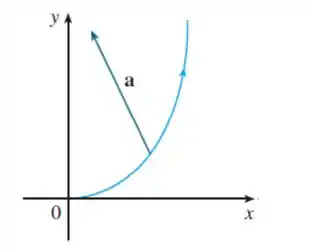
Passo 1
Então, galera. Para resolvermos essa questão, não tem jeito, infelizmente....Vamos ter que contar com uma régua pra medir algumas coisas. 
O que vamos medir?
A questão nos dá apenas o valor do vetor aceleração e nos pede para calcular a aceleração normal e tangencial. Mas vamos parar para pensar... Não dá para calcular apenas com uma informação!!! O que podemos fazer?
Utilizamos a régua e medimos os vetores, e com eles podemos fazer uma regra de três. O módulos dos vetores são proporcionais aos seus comprimentos:
Vamos começar?
Passo 2
Bom....Precisamos projetar o vetor aceleração numa linha tangente à curva para determinarmos a sua componente tangencial e... projetar o vetor aceleração numa linha normal à curva para determinarmos a sua componente normal .
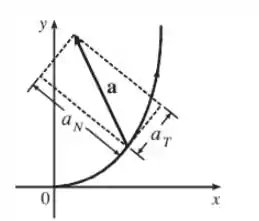
Passo 3
Agora precisamos medir os comprimentos dessas projeções e comparar com o comprimento do vetor original de aceleração. Como sabemos que este último vetor corresponde a uma aceleraç��o de de magnitude, basta fazer uma regra de 3 para determinarmos o valor dessas componentes.
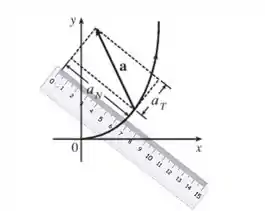
Vetor aceleração normal mede :
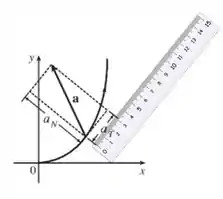
Vetor aceleração tagencial mede :
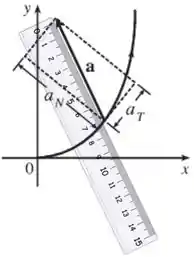
Vetor aceleração mede :
Passo 4
Agora que encontramos a medida dos vetores podemos fazer uma regra de três para encontrar a a aceleração normal.
Multiplicando “cruzado”, temos o valor de
Passo 5
Com isso a aceleração tangencial será
Multiplicando “cruzado”, temos o valor de