Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 3.16 - Ex. 3d
Analisar graficamente a existência de assíntotas para as seguintes funções:
Passo 1
O gráfico dessa função fica assim:
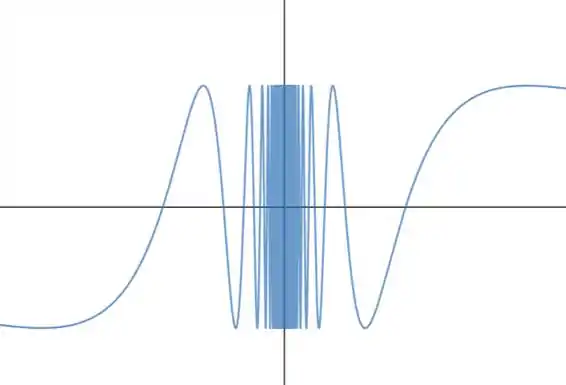
Passo 2
Esse meio aí fica parecendo uma mola, e pelo menos nesse pedaço não dá pra ver assíntota nenhuma... Mas tirando o zoom a assíntota aparece!
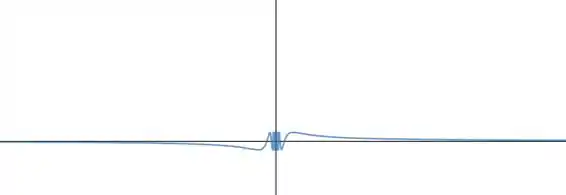
Daí, é a assíntota horizontal.
Resposta
é uma assíntota horizontal.
Exercícios de Livros Relacionados
33. Encontre o limite ou demonstre que não existe. lim x → ∞ a r c t g e x
41. Encontre as assíntotas horizontais e verticais de cada curva. Confira seu trabalho por meio de um gráfico da curva e das estimativas das assíntotas. y = 2 x + 1 x - 2
45. Encontre as assíntotas horizontais e verticais de cada curva. Confira seu trabalho por meio de um gráfico da curva e das estimativas das assíntotas. y = x 3 - x x 2 - 6 x + 5
36. Encontre o limite ou demonstre que não existe. lim x → ∞ s e n 2 ( x ) x 2 + 1
44. Encontre as assíntotas horizontais e verticais de cada curva. Confira seu trabalho por meio de um gráfico da curva e das estimativas das assíntotas. y = 1 + x 4 x 2 - x 4