Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 3.16 - Ex. 3c
Analisar graficamente a existência de assíntotas para as seguintes funções:
Passo 1
Quando plotei o gráfico dessa função já tomei um susto!
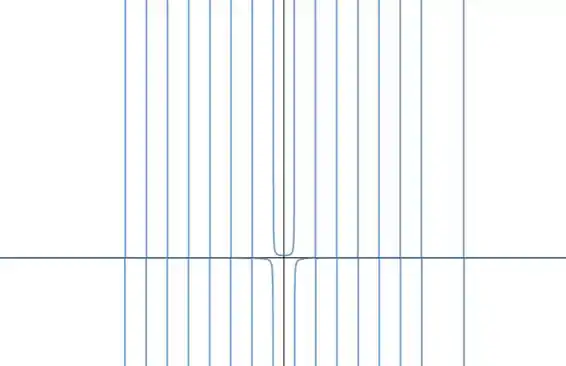
Tá louco, mó gráfico feio...
Passo 2
Analisando o gráfico, já vemos de cara que é uma assíntota horizontal. Além dessa, tem essas várias assíntotas verticais aí, que aparecem por causa da tangente, pros valores que são congruentes (trigonometricamente) a e .
Resposta
é uma assíntota horizontal e temos diversas assíntotas verticais.
Exercícios de Livros Relacionados
Nos Exercícios 3-8, determine o limite de cada função a) quando x → ∞ e b) quando x → - ∞ . 3) f x = 2 x - 3
Nos Exercícios 3-8, determine o limite de cada função a) quando x → ∞ e b) quando x → - ∞ . 6) f x = 1 8 - 5 x 2
Nos Exercícios 3-8, determine o limite de cada função a) quando x → ∞ e b) quando x → - ∞ . 4) f x = π - 2 x 2
Para a função f cujo gráfico é dado, determine os seguintes limites. lim x → 2 f ( x ) lim x → - 3 + f x lim x → - 3 - f x lim x → - 3 f x lim x → 0 + f x lim x → 0 - f x lim x → 0 f x l
Determine o limite de cada função b) quando QUOTE _x0001_