Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.1 - Ex. 33
Analise as funções trigonométricas nos intervalos especificados indicando onde é crescente, decrescente, côncava para cima, côncava para baixo, e as coordenadas de todos os pontos de inflexão. Verifique se seus resultados estão em conformidade com o gráfico de gerado por algum recurso computacional.
33.
Passo 1
Peguemos o gráfico da função, dentro do intervalo pedido, pra já termos uma melhor ideia dos nossos resultados:
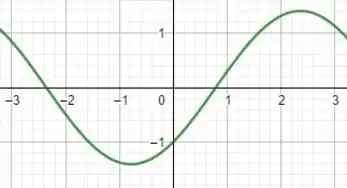
Passo 2
vai ser crescente entre os pontos de mínimo e os pontos de máximo, nesta ordem, necessariamente. Pra determiná-los, precisamos derivar a função e igualar a derivada a zero.
Temos:
Igualando a zero, vamos ter:
Do ciclo trigonométrico, essa correlação vai ocorrer no ângulo de e em todos os arcos que distem desse ângulo ( é um número inteiro qualquer). Dá uma conferida, certeza que você vai relembrar e entender bem!
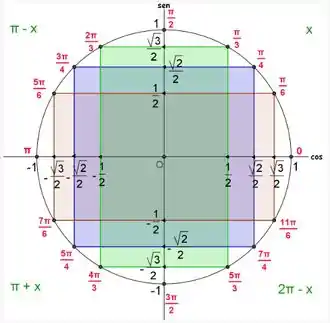
Pelo gráfico, verificamos que a função tem um ponto de máximo aproximadamente perto de . Esse ponto corresponde justamente a .
Como nos interessa o ponto de mínimo, basta subtrairmos desse ponto, já que as funções seno e cosseno (mesmo compostas) originalmente têm como período o valor de . Assim, a distância entre uma crista e um vale, meio período, equivale a .
Temos:
Assim, o intervalo em que a função é crescente será:
Passo 3
Como estamos restritos ao intervalo , e vemos pelo gráfico que, desde a função decresce. Logo, ela vai ser decrescente desde até o ponto de mínimo, em , e também a partir do ponto de máximo, em até . Teremos como o intervalo em que a função decresce:
Passo 4
Pra verificar os intervalos de concavidade voltada pra cima e pra baixo, precisamos dos pontos de inflexão, que se determinam quando igualamos a derivada segunda da função a zero.
Temos:
Igualando a zero, vamos ter:
Do ciclo trigonométrico, essa correlação ocorre no ângulo de e em todos os arcos que distam desse ângulo.
No intervalo em que estamos restritos, observamos dois pontos de inflexão, que também distam um do outro. O primeiro, com coordenada negativa equivalerá ao ponto de inflexão subtraído de :
Assim já temos as coordenadas dos pontos de inflexão, em e em
Passo 5
Observando pelo gráfico, a função, desde é côncava pra baixo, e assim será até o primeiro ponto de inflexão em .
Nisso, ela passa a ser côncava pra cima, até o segundo ponto de inflexão, em .
Logo em seguida, retorna à concavidade voltada pra baixo.
Sintetizando isso em intervalos, vamos ter:
Concavidade voltada pra baixo:
Concavidade voltada pra cima:
Resposta
Ei, a resposta está no passo a passo :)