Use um recurso computacional para aproximar a solução da equação. Quando forem usados radianos, expresse sua resposta com quatro casas decimais; quando forem usados graus, expresse-a até o décimo de grau mais próximo. [Nota: Em cada parte, a solução não está na imagem da função trigonométrica inversa pertinente.]
Passo 1
Fala galera, tudo certo? Vambora! Olha só, pra letra , a questão pede a solução aproximada de:
Ou seja, ela quer um valor de nesse intervalo que satisfaça a igualdade. Pô, parece tentador fazer:
Né não? Mas o enunciado já nos deu o bizu de que isso não vai dar certo. Bem, já que é assim, vamos tentar então usar um recurso computacional pra resolver. Eu recomendo usar uma ferramenta de planilhas e escolher alguns valores de pra ver quanto dá o seno deles. Com a escolha de alguns , achamos esses valores de seno:
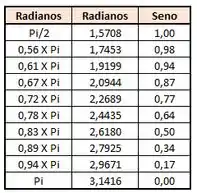
E veja só! O seno de valor está entre e radianos. Podemos interpolar então pra achar em qual radiano o seno de valor está:
Multiplicando cruzado, temos:
Usando a mesma ferramenta de planilhas pra fazer essa conta, achamos o seguinte valor de :
Passo 2
Galera, aqui é a mesma coisa, só que vamos trabalhar só com graus:
Podemos montar uma tabelinha também, saca só:
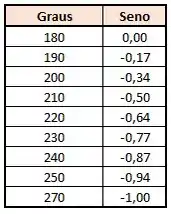
Veja que está entre e ! Interpolando de novo, temos:
Multiplicando cruzado, temos:
Usando a mesma ferramenta de planilhas pra fazer essa conta, achamos o seguinte valor de :