Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.3 - Ex. 12-a
12 . Um recém-formado pegou emprestado o valor de R$ 150.000,00 a uma taxa de juros de 6% aoano para comprar um apartamento. Antecipando constantes aumentos de salário, ele esperapagar a uma taxa mensal de 800 + 10t, em que t é o número de meses desde o início doempréstimo.(a) Supondo que o programa de pagamento possa ser mantido, quando o empréstimo estaráquitado?(b) Supondo o mesmo programa de pagamento, qual deve ser a quantia emprestada para que seja paga em exatamente 20 anos?
Passo 1
- No inicio da seção deste capitulo descobrimos que a equação que rege juros com aportes constantes é
Onde S(t) é o montante, C nossa constante arbitraria, k as parcelas e o valor do nosso juros. Assim pelas condições do nosso problema, podemos dizer que
Temos que trabalhar aqui com juros mensais, afinal pagamos mensalidades do imóvel. A parte dos juros pode ser uma questão de complicação. Afinal temos uma taxa anual de 6%. Por propriedades de exponencial não podemos fazer nem pois não resultam em valores de juros acurados. Temos que adicionar 1 a r e fazer a conta , e como a equação requer apenas r, subtraímos 1 ao final. Blz? Vamos achar então nosso valor da constante arbitraria C
Passo 2
Isso faz com que nossa equação fique assim
Passo 3
Agora queremos saber t para que , então bora calcular
É galera, nem tudo são flores, e infelizmente. Essa função não tem solução analítica, a solução será por método geométrico. Vamos plotar o gráfico de
E ver os pontos onde ele cruza
E com isso conseguimos
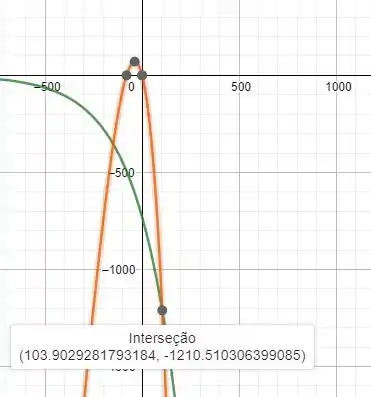
Ou seja, nosso tempo é
Terminamos por aqui. Te vejo na próxima resolução
: )