Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 5.2 - Ex. 40
Aproxime a integral a uma soma de áreas:
Passo 1
Fala aí galera, bora pra mais um problema de cálculo! Temos que achar uma área que seja equivalente a seguinte integral:
Vamos começar analisando o esboço do gráfico:
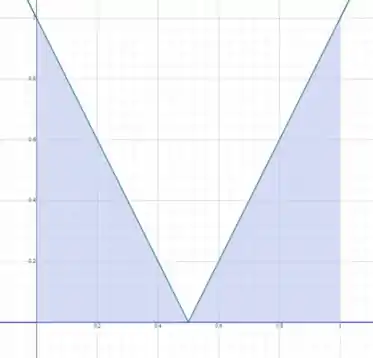
A nossa integral se refere à parte hachurada do gráfico. Se você reparar a gente tem dois triângulos retângulos, então temos que calcular a soma de suas áreas!
Passo 2
A fórmula da área de um triângulo é:
Para sabermos a base de cada triângulo, vamos precisar calcular a raiz da função:
O retângulo mais a esquerda tem uma base que vai do eixo até e sua altura pode ser calculada por . Assim:
Para o triângulo a direita temos uma base que vai de até e :
A área total fica:
Logo:
Prontinhoo!
Resposta
Exercícios de Livros Relacionados
Suponha que f tenha uma valor mínimo absoluto m e um valor máximo absoluto M . Entre quais dois valores ∫ 0 2 f x d x deve ficar? Que propriedade das integrais lhe permitem tirar esta conclusão?
Use as propriedades das integrais para verificar a desigualdade sem calcular as integrais. 2 ≤ ∫ - 1 1 1 + x 2 d x ≤ 2 2
Use a Propriedade 8 para estimar o valor da integral. ∫ 0 2 x 3 - 3 x + 3 d x
Se f for contínuaem [a , b] , mostre que|int_a^b f (x) d x| = int_a^b |f (x)| d x [Sugestão: - |f (x)| = f (x) = |f (x)| .]
Use as propriedades das integrais para verificar a desigualdade sem calcular as integrais. 2 π 24 ≤ ∫ π 6 π 4 cos xd x ≤ 3 π 24