Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.7 - Ex. 1
Aproxime a integral usando (a) a aproximação pelo ponto médio, (b) a aproximação trapezoidal e (c) a aproximação pela regra de Simpson usando a Fórmula (7). Em cada caso, encontre o valor exato da integral e aproxime o erro absoluto. Expresse suas respostas com pelo menos quatro casas decimais.
Passo 1
A ideia aqui é que vamos aproximar o valor dessa integral por diferentes métodos e comparar com o valor absoluto. Vamos calcular esse valor exato da integral então. Podemos usar a substituição:
Os limites de integração ficam assim:
E a integral fica:
Passo 2
(a) Para calcular a aproximação pelo ponto médio, precisamos usar essa fórmulinha:
Como no nosso caso , e :
Passo 3
Só precisamos calcular esses valores de . O tamanho dos nossos intervalos é , então podemos chamar:
E dizer que:
Aí fazendo isso para valores de entre e , e substituindo na nossa fórmulinha:
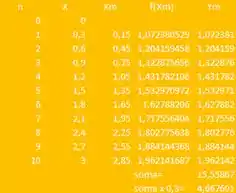
Comparando com o valor exato:
Passo 4
(b) A aproximação trapezoidal tem essa forma:
Como no nosso caso , e :
Sendo:
Onde . Variando esse valor de entre e , descobrimos que:
Comparando com o valor exato:
Passo 5
(c) A fórmula (7) diz que:
Já que queremos , podemos dizer que:
E esses valores a gente já tem. Só substituir:
Comparando com o valor exato:
Repara que não quer dizer que os valores são iguais, mas que o erro é menor do que o número de casas decimais que a gente está usando, tranquilo?