Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.3 - Ex. 84
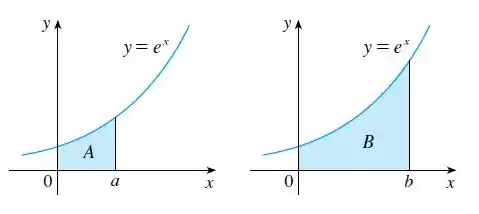
A área marcada B é três vezes a área marcada A. Expresse b em termos de a.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos dá os seguintes gráficos que mostram duas áreas hachuradas e :
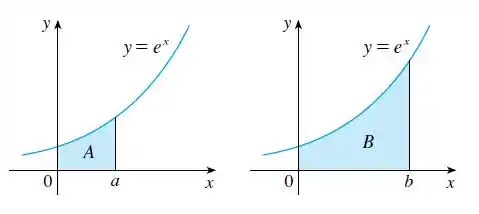
Queremos expressar em termos de .
Cuidado!! Estamos falando dos limites de integração e não sobre expressar em termos de (até porque o enunciado já nos diz que )!!
Bom... Se lembram como calcular a área abaixo de um gráfico?
Usando a integral, não é?
Então bora aplicar!! 😉
Passo 2
Pelo Teorema Fundamental do Cálculo, sabemos que:
Parte 1:
Se for contínua em , então a função definida por
É contínua em e derivável em e .
Parte 2:
Se for contínua em , então
Onde é qualquer primitiva de , isto é, uma função tal que .
Passo 3
Assim, aplicando em , temos:
Integrando:
Aplicando os limites:
Aplicando a distributiva:
Aplicando o em ambos os lados:
Então:
Entendeu direitinho?? Responde aee😉