Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.Revisão - Ex. 26

Dê um argumento geométrico para calcular:

int_0^1 |2 x - 1| d x

Passo 1

A primeira coisa que faremos é analisar quando a função dentro do módulo será nula:

2 x - 1 = 0

2 x = 1

x = (1)/(2)

O intervalo fornecido pelo exercício é de 0 até 1 , onde 0 <= x <= 1 . Mas, no meio desse intervalo a função é nula, isso significa que vamos dividir em dois intervalos importantes, um extremo esquerdo onde teremos valores estritamente negativos dentro do módulo e outro a direita, onde os valores são positivos. O primeiro intervalo será:

0 <= x <= (1)/(2)

E também :

(1)/(2) <= x <= 1

Agora, podemos resovelr a integral:

int_0^1 |2 x - 1| d x = int_0^(1 // 2) - ( 2 x - 1 ) d x + int_(1 // 2)^1 ( 2 x - 1 ) d x

Assim, conseguimos resolver a integral!

Passo 2

Vamos primeiro resolver a integral negativa, onde:

int_0^((1)/(2)) - (2 x - 1) d x = int_0^(1 // 2) - 2 x + 1 d x

Lembrando que a integral da subtração ou soma, é a subtração ou soma das integrais:

int_0^((1)/(2)) - 2 x + 1 d x = int_0^((1)/(2)) - 2 x d x + int_0^((1)/(2)) 1 d x

int_0^(1 // 2) - 2 x + 1 d x = [ - x^2 ]_0^(1 // 2) + [ x ]_0^(1 // 2) = - (1)/(4) + (1)/(2) = (1)/(4)

Então, temos a primeira integral.

Passo 3

Agora, resolveremos a integral positiva, onde:

int_((1)/(2))^1 (2 x - 1) d x = int_((1)/(2))^1 2 x - 1 d x

Lembrando que a integral da subtração ou soma, é a subtração ou soma das integrais:

int_((1)/(2))^1 2 x - 1 d x = int_((1)/(2))^1 2 x d x - int_((1)/(2))^1 1 d x

int_((1)/(2))^1 2 x - 1 d x = [ x^2 ]_(1 // 2 )^1 - [x]_((1)/(2))^1 = [1 - (1)/(4)] - [1 - (1)/(2)] = (3)/(4) - (1)/(2) = (1)/(4)

Feito isso, vamos pra parte final do exercício.

Passo 4

Retornando ao nosso foco principal que é resolver a integral:

int_0^1 |2 x - 1| d x = int_0^(1 // 2) - ( 2 x - 1 ) d x + int_(1 // 2)^1 ( 2 x - 1 ) d x

Agora, com os termos calculados separamente, temos:

int_0^1 |2 x - 1| d x = (1)/(4) + (1)/(4) = (2)/(4) = (1)/(2)

int_0^1 |2 x - 1| d x = (1)/(2) = 0,5

Analisando graficamente, temos:

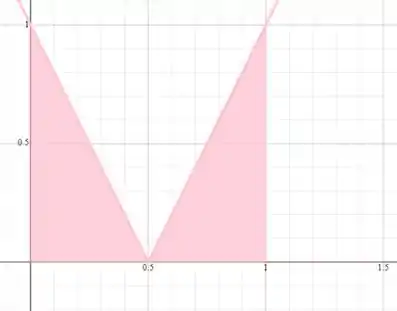
A área colorida no gráfico é a área calculada pela integral.

Resposta

int_0^1 |2 x - 1| d x = (1)/(2) = 0,5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Denote por D = D a um disco de raio a submerso em um fluido de peso específico ρ de tal maneira que o centro de D esteja h unidades abaixo da superfície do fluido. Para cada valor de r no interval
23-26 Encontre a massa e o centro de gravidade da lâmina dada de densidade δ .24. A lâmina delimitada pelo gráfico x = y 4 e a reta x = 1 ; δ = 15 .
21.Use considerações de simetria para argumentar que o centroide de um triângulo isósceles fica na mediana da base do triângulo.
31-34 Verdadeiro/Falso Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta [No exercício 34, suponha que o quadrado girado fique no plano x yà à direitado eixo y ] 32. O centroi
31-34 Verdadeiro/Falso Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta [No exercício 34, suponha que o quadrado girado fique no plano x yà à direitado eixo y ] 33. O centroi