Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.2 - Ex. 27
Associe aa função representada graficamente uma derivada das Figuras (a)-(d) a seguir.
Passo 1
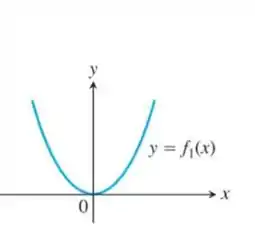
Primeiro, devemos notar que no vértice da parábola, a reta tangente é constante, ou seja, o coeficiente angular é nulo. Portanto, no ponto a derivada deve ser zero.
Note que a angulação das retas tangentes aumenta conforme o aumento de .
Passo 2
Em seguida, note que a angulação das retas tangentes aumenta conforme o aumento de . A angulação inicia negativa e, logo após o vértice da parábola, se torna positiva.
Passo 3
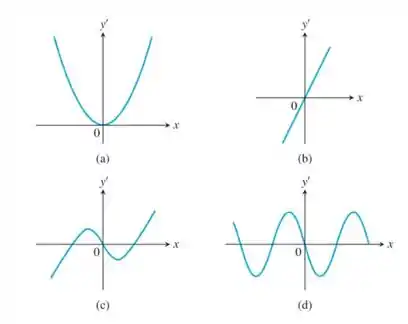
Por fim, devemos perceber que o único gráfico de derivada que corresponde às interpretações observadas nos passos anteriores é o gráfico representado no item (b)
Resposta
Item (b).
Exercícios de Livros Relacionados
42) Dada f x = 10 x 2 Use uma calculadora para tabular valores de f 5 + ∆ x - f ( 5 ) ∆ x quando ∆ xé1 ,0,5 ,0,1 ,0,01 ,0,001 , e∆ xé - 1 ,- 0,5 ,- 0,1 ,- 0,01 ,- 0,001 é é . A que f 5 + ∆ x - f ( 5 )
A área da região limitada pela curva y = e - x , pelos eixos coordenados e pela reta x =b (b0) é uma função de b. Se f for essa função , ache f(b). Ache também lim b → ∞ f ( b )
O volume de um solido de revolução da região limitada pela curva y = e - x , pelos eixos coordenados e pela reta x =b (b0) é uma função de b. Se g for essa função , ache g(b). Ache também lim b → ∞
Uma partícula move-se sobre uma reta , sendo s a distancia orientada da partícula a partir da origem , V m/s, a velocidade da partícula e A m/s² , a aceleração da partícula, t s. Se a = e t + e - t ,
Ache a equação da reta tangente à curva y = x x - 1 em (2,2)