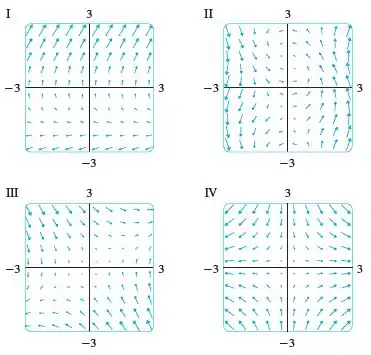
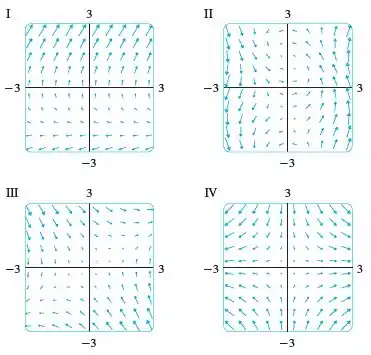
Associe os campos vetoriais com os gráficos rotulados I-IV. Dê razões para suas escolhas.
Passo 1
Faaala turma, tudo bem?
Devemos analisar o campo e identificar qual dos gráficos de I a IV o representa.
Como vamos resolver esse tipo de problema?
Para resolver o problema vamos analisar como o campo se comporta em cada quadrante, como também testar alguns pontos para confirmarmos nossa suposição.
Utilize essa figura como referência, para identificar cada quadrante:
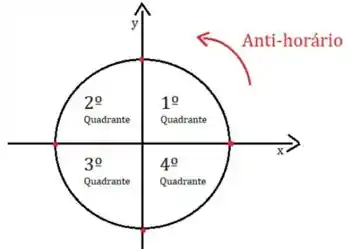
Vamos nessa!!!
Passo 2
Repare na expressão:
Temos que nosso campo para todo valor de positivo, terá a componente da direção positiva.
Essa figura irá nos ajudar a entender os quadrantes:
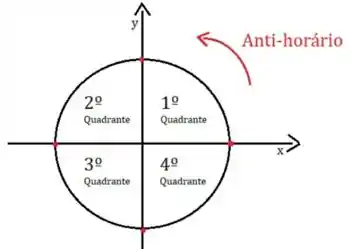
Sendo assim, temos que para os quadrantes e os vetores estarão tendendo a apontar para cima.
Já quando assumi valores negativos, teremos que a componente será negativa, assim o quadrante e será tendendo para baixo.
Com essas informações, vamos analisar as figuras:
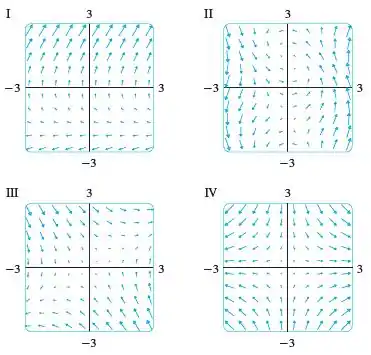
Assim, chegamos à conclusão então que o gráfico que mais se identifica com nosso campo é o gráfico .
Resposta
Gráfico