Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.1 - Ex. 12
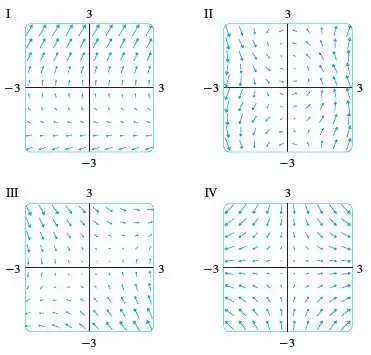
Associe os campos vetoriais com os gráficos rotulados I-IV. Dê razões para suas escolhas.
Passo 1
E aiiiii galerinha, tudo na paz?
Precisamos associar o campo com algum dos gráficos de I-IV, e justificar a escolha.
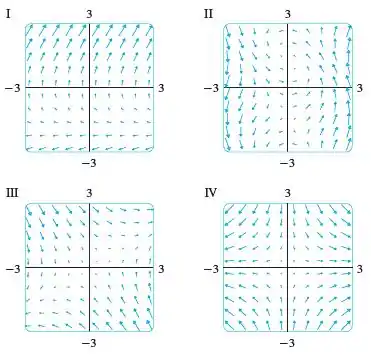
Para resolver o problema vamos montar uma tabela com alguns valores e ver como o campo se comporta em alguns pontos específicos.
Faça com os seguintes pontos:
Avalie também, como o vetor se comporta com pontos iguais. Por exemplo:
Primeiro quadrante: (1,1), (2,2), (3,3)
Terceiro quadrante: (-1,-1), (-2,2), (-3,3)
Devemos também fazer uma interpretação da norma do campo para descobrirmos como se comporta o tamanho do vetor para os valores.
Vamos nessa!!
Passo 2
Vamos começar montando uma pequena tabela e escolher os seguintes pontos aleatoriamente:
Agora vamos aplicar cada ponto em :
Respectivamente, para cada ponto, temos que nosso campo vetorial se comporta da seguinte forma:
Note o seguinte:
O campo tem um comportamento de afastamento da origem no primeiro e terceiro quadrante.
Para os pontos:
Temos:
Note agora que no segundo e quarto quadrante os vetores se aproximam da origem.
Passo 3
Vamos observar o comportamento do campo elétrico para as seguintes situações.
Primeiro quadrante: (1,1), (2,2), (3,3)
Terceiro quadrante: (-1,-1), (-2,2), (-3,3)
Vamos aplicar em
Primeiro quadrante:
Terceiro quadrante:
Observe que para pontos positivos iguais primeiro quadrante, os vetores estarão sempre apontando para direita, enquanto que para o terceiro quadrante os vetores estarão apontando para a esquerda.
Passo 4
Por fim, vamos analisar a norma do campo:
Vemos então que quanto menor os valores para e , menor será o tamanho do vetor, ou seja, quanto mais próximo da origem menor o tamanho dos vetores.
Com todas essas informações, e analisado os gráficos:
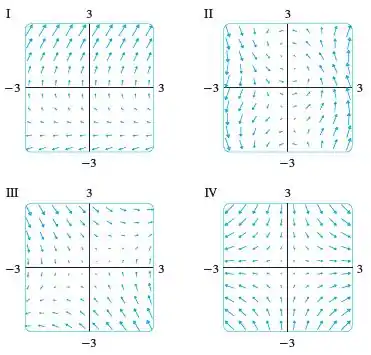
Chegamos à conclusão então que o gráfico que mais se identifica com nosso campo é o gráfico .
Resposta
Gráfico