Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.6 - Ex. 49
Se , encontre o vetor gradiente e use-o para encontrar a reta tangente à curva de nível no ponto . Esboce a curva de nível, a reta tangente e o vetor gradiente
Passo 1
Bora lá galera. Pra começo de conversa, vamos pensar no vetor gradiente. Pela definição:
Onde e são, respectivamente, as derivadas parciais em relação a e de . Belê! Nosso enunciado nos deu:
Então as derivadas parciais serão:
Portanto nosso vetor gradiente é:
E vetor gradiente que o enunciado pediu será:
Passo 2
Show de bola galera, agora vamos pontar a reta tangente. Pra isso, vamos lembrar da modelagem dela:
Pô, o ponto nada mais é do que o ponto de tangência, dado do enunciado, e é o vetor diretor dessa reta, que vamos descobrir. Seja:
Como representa o vetor diretor da reta normal a curva de nível no ponto , e retas normais e tangentes são perpendiculares, podemos lembrar da propriedade do produto escalar de vetores perpendiculares:
E logo:
O vetor diretor tem então essa expressão:
Arbitrando um valor qualquer de , como por exemplo, , achamos:
E taí galera! Sendo o ponto de tangência , nossa reta tangente será:
Passo 3
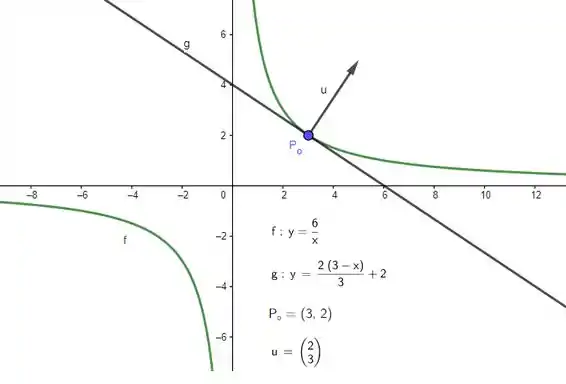
Agora a gente esboça tudo! Pra começar, se a curva de nível ocorre em:
Basta a gente esboçar no a curva:
Marcar o ponto . Fazer a reta tangente:
E marcar o vetor normal a curva de nível no ponto , que nada mais é do que um vetor com as direções do gradiente, isto é, . Juntando isso tudo no gráfico, temos:
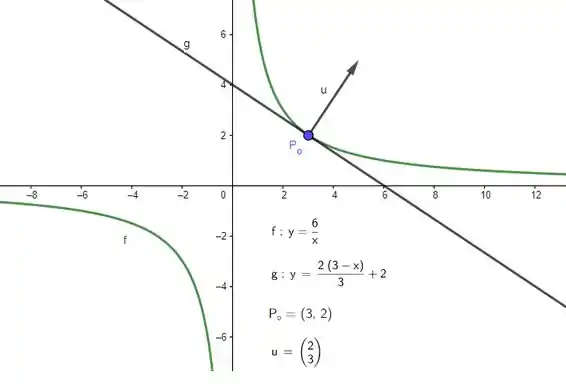
Resposta
