Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.2 - Ex. 28
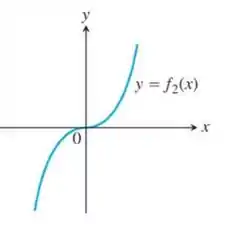
Associe a função representada graficamente uma derivada das Figuras (a)-(d) a seguir.
Passo 1
Primeiro, devemos notar que no ponto do gráfico a reta tangente à curva é constante. Portanto, a derivada no ponto deve ser nula.
Passo 2
Em seguida, é necessário perceber que não há outros pontos nos quais a reta tangente é constante; portanto, a curva da derivada deve ter apenas um zero.
Passo 3
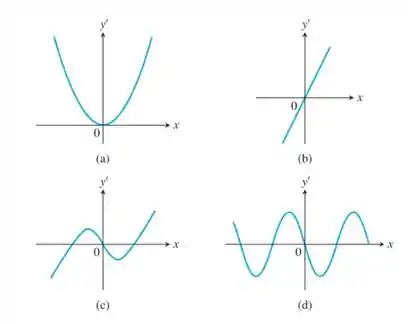
Analisando as observações feitas nos passos anteriores, devemos notar que o gráfico se enquadra é o gráfico do item (a).
Resposta
Item (a).
Exercícios de Livros Relacionados
Faça o Exercício 65 da série de Exercícios de Revisão do Capítulo 5, calculando todas as integrais.Exercício 65) Mostre que cada uma das desigualdades é válida: c ) ∫ 4 5 d x x - 3 ≥ ∫ 4 5 d x x
Prove que se x0 e ∫ 1 x t h - 1 d t = 1 , então lim h → 0 x = lim h → 0 1 + h 1 h
Faça o Exercício 65 da série de Exercícios de Revisão do Capítulo 5, calculando todas as integrais.Exercício 65) Mostre que cada uma das desigualdades é válida: b ) ∫ 1 2 d x x ≥ ∫ 1 2 d x x - 3
Ache ∫ 0 t e - | x | . d x Se t for um número real qualquer.
Faça o Exercício 65 da série de Exercícios de Revisão do Capítulo 5, calculando todas as integrais.Exercício 65) Mostre que cada uma das desigualdades é válida: a ) ∫ - 2 - 1 d x x - 3 ≥ ∫ - 2 - 1 d x