Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.1 - Ex. 24

Esboce o gráfico de à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de .

Passo 1

Oieee, bora resolver mais uma comigo????

Vamos esboçar o gráfico da funçãono intervalo e determinar os valores máximos e mínimos locais e absolutos.

Vamos analisar a Função

A funçãotem um comportamento comportamento particular em relação aos seus valores e assíntotas verticais:

é definida para todos os valores de exceto quando , onde a tangente tende ao infinito.
A função tem um ponto notável em onde .
No intervalo , a tangente passa de valores negativos para positivos e tende ao infinito conforme se aproxima de

Os pontos críticos dentro do intervalo são as extremidades do intervalo e o vértice da parábola .

Para :

Para

Para próximo de (mas não inclui ):

Passo 2

Para esboçar o gráfico de no intervalo

1. Plote o ponto

2. Indique a tendência do gráfico para conforme se aproxima de .

- Máximo absoluto: Não há valor máximo absoluto no intervalo porque a função tende ao infinito conforme se aproxima de .

- Mínimo absoluto: O valor mínimo absoluto ocorre em

Passo 3

Para desenhar o gráfico à mão:

1. Plote o ponto

2. Desenhe a curva que passa por esses pontos e tende ao infinito à medida que se aproxima de .

Gráfico:

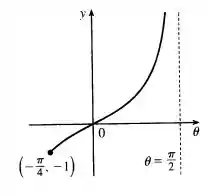
Passo 4

- Máximo absoluto: Não existe um valor máximo absoluto porque a função tende ao infinito.- Mínimo absoluto: .

Dentro do intervalo a função tem um valor mínimo absoluto de em e não possui um valor máximo absoluto porque a função tende ao infinito conforme se aproxima de . Não há outros máximos ou mínimos locais dentro deste intervalo.