Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 5
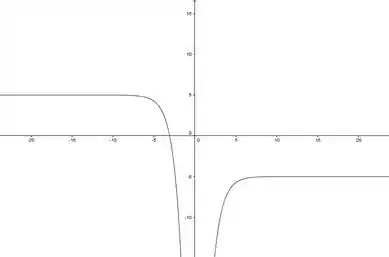
5. Esboce o gráfico de um exemplo de uma função que satisfaça a todas as condições dadas:
Passo 1
Opa, vamos fazer essa questão! O enunciado pede pra a gente esboçar um gráfico de levando em conta que:
Para isso, precisaremos lembrar do que são as assíntotas horizontais e verticais!!
Basicamente as assíntotas são linhas imaginárias que uma função se aproxima à medida que a variável independente se aproxima de valores específicos.
As assíntotas horizontais são linhas horizontais que a função se aproxima à medida que a variável independente se aproxima de infinito positivo ou negativo.
Já as assíntotas verticais são linhas verticais que a função se aproxima à medida que a variável independente se aproxima de um valor específico.
Geralmente, esses valores são aqueles para os quais a função não está definida, como pontos de descontinuidade ou divisões por zero.
Agora bora aplicar!! 😉
Passo 2
Logo de cara a gente consegue identificar que e são assíntotas horizontais em e .
Oxente... como assim assíntotas horizontais??
Pra a gente saber você só precisa imaginar que você está desenhando um gráfico com valores cada vez maiores (ou menores, no caso de ) e o continua ali pertinho de um valor fixo!
Isso não te parece uma graaande linha?! Pois é!! Trata-se de uma assíntota!!
Passo 3
Agora, no caso de temos uma é uma assíntota vertical em , é só você fazer o mesmo raciocínio.
Você está desenhando seu gráfico e do nada chega perto de um valor de onde fica gigantão! Isso vai ter um formato parecido com uma reta vertical, que é a assíntota!
(é parecido, não igual, beleza?!)
Passo 4
Resumindo temos:
- Assíntota horizontal em para
- Assíntota horizontal em para
- Assíntota vertical em para
Agora é só colocar a imaginação pra jogo e desenhar o gráfico:
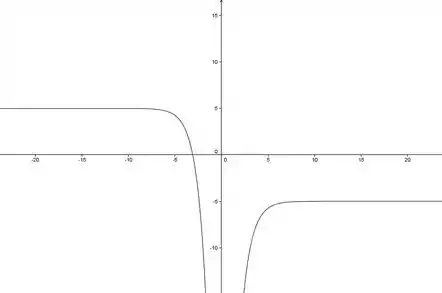
Perceba que quando se aproxima de , passa a ter valores muito negativos.
Por outro lado, quando a gente tem valores de muito grandes, fica ali perto de .
Por fim, quando temos valores grandes negativos de , o se aproxima de .
Resposta
