Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 7.2 - Ex. 49

Avalie a integral indefinida. Ilustre e verifique se a sua resposta é razoável colocando em um gráfico o integrando e sua antiderivada (C=0).

∫ sin 5 ⁡ x d x

Passo 1

Para resolver esse probleminha é bem fácil! Só aplicarmos uma substituição trigonométrica. Vamos ver:

Podemos tornar o seno aplicando sin 2 ⁡ x + cos 2   ⁡ x = 1 , da seguinte forma:

∫ 1 - cos 2 ⁡ x 2 si n ⁡ x d x

Pronto, mas ainda não tá tudo certo! Por isso fazemos uma substituição:

u = cos ⁡ x                         d u = - sin ⁡ x d x

Agora ta bom demais!!

Passo 2

Resolvendo o produto notável e aplicando a substituição na integral, temos

∫ ( 1 - 2 cos 2 ⁡ x + cos 4 ⁡ x ) ( - d u )

Resolvendo a integral, fica assim:

∫ ( - 1 + 2 u 2 - u 4 ) d u = - u + 2 u 3 3 - u 5 5 + C

Substituindo o nosso valor de u :

∫ sin 5 ⁡ x d x = - cos ⁡ x + 2 c o s 3 x 3 - c o s 5 x 5 + C

Analisando o gráfico, sendo a curva de cor preta o resultado da nossa integral, temos:

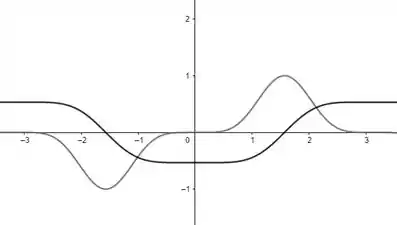
Observe que F está aumentando quando   f x > 0 , portanto, os gráficos servem como uma verificação do nosso trabalho.

Finishh!! :)

Resposta

∫ sin 5 ⁡ x d x = - cos ⁡ x + 2 c o s 3 x 3 - c o s 5 x 5 + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios 1 a 30, calcule a integral indefinida:6. ∫ t g 4 x d x
Nos exercícios 1 a 30, calcule a integral indefinida:8. ∫ c o t g 5 2 x d x
Nos exercícios 1 a 30, calcule a integral indefinida:7. ∫ t g 6 3 x d x
Calcule a integral definida. ∫ 0 π cos 3 ⁡ xd x
Calcule a integral definida. ∫ 0 2 π s e nx - cos ⁡ xd x