Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.4 - Ex. 34
Um avião está voando a uma altitude constante e com uma velocidade constante de . Um míssil antiaéreo é disparado em uma linha reta perpendicular à trajetória de voo do avião, de tal forma que irá atingi-lo em um ponto (ver figura abaixo). No instante em que o avião está a do ponto de impacto, o míssil está a dele e voando a. Naquele instante com que rapidez estará decrescendo a distância entre o míssil e o avião?
Passo 1
Vamos ver um desenho melhor pra entender o que está acontecendo? Hehe
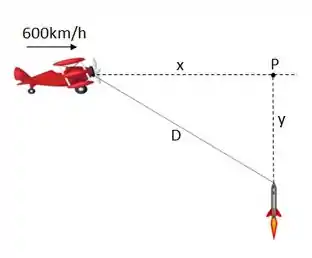
Para um instante qualquer, vamos chamar de a distância entre o míssil e o avião, de a distância entre o avião e o ponto e de de a distância entre o míssil e o ponto .
Pelo Teorema de Pitágoras podemos falar que:
Podemos derivar em relação ao tempo essa expressão pra relacionar as taxas de variação desses caras:
Pela Regra da Cadeia:
Passo 2
O enunciado nos diz que o avião está voando com uma velocidade constante de Daí podemos tirar que
Lembrando que como o avião se aproxima do ponto , a distância está DIMIUINDO, por isso o sinal de menos.
Além disso o míssil está voando a , ou seja:
O sinal negativo pelo mesmo motivo do anterior.
Passo 3
No instante desejado o avião está a do ponto de impacto, o míssil está a dele. Então e . A partir disso conseguimos achar o valor de
Substituindo todos esses dados na equação (1):
Repare que encontramos um , o que faz bastante sentido uma vez que a distância entre o avião e o míssil está diminuindo 😊