Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.4 - Ex. 22

Para a câmera e o foguete da Figura 3.4.5, a que taxa estará subindo o foguete quando o ângulo de elevação for de π / 4 radianos e se estiver crescendo a uma taxa de 0,2   r a d / s ?

Passo 1

A Figura 3.4.5 é a seguinte:

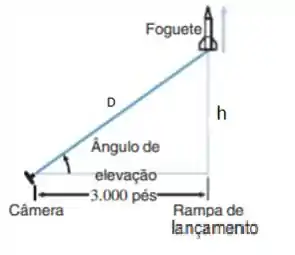
Chamando a distância entre o foguete e a câmera de D , usando o ângulo de elevação π / 4 , podemos falar que:

cos ⁡ π 4 = 2 2   = 3000 D                                     ⇒                         D = 3000 2   p é s

Passo 2

Chamando o ângulo de elevação de θ , podemos falar que num instante genérico:

sin ⁡ θ =   â n g u l o   o p o s t o h i p o t e n u s a =   h D

Aonde h é a altura do avião nesse instante genérico.

Derivando essa expressão em relação ao tempo, vamos chegar no seguinte:

sin ⁡ θ =   h D                 ⇒         D sin ⁡ θ = h

d d t ( D sin ⁡ θ ) = d h d t

Usando a derivada do produto:

D d sin ⁡ θ d t + sin ⁡ θ d D d t = d h d t

Pela regra da cadeia:

D cos ⁡ θ d θ d t + sin ⁡ θ d D d t = d h d t

d D d t = 1 sin ⁡ θ     d h d t - D cos ⁡ θ d θ d t                         e q u a ç ã o   ( 1 )

Passo 3

Mas aí apareceu um tal de d D / d t   que não sabemos, mas pra relacionar ele, podemos falar que:

cos ⁡ θ = c a t e t o   a d j a c e n t e h i p o t e n u s a =   3000 D    

Derivando essa expressão em relação ao tempo, vamos chegar no seguinte:

cos ⁡ θ =   3000 D                     ⇒             D cos ⁡ θ = 3000  

d d t ( D cos ⁡ θ ) = d ( 3000 ) d t  

Pela derivada do produto:

d D d t cos ⁡ θ + D   d cos ⁡ θ d t = d ( 3000 ) d t

Mas derivada de constante é zero. Então usando a regra da cadeia:

d D d t cos ⁡ θ - sin ⁡ θ D   d θ d t = 0  

d D d t = D ⁡   sin ⁡ θ cos ⁡ θ d θ d t                         e q u a ç ã o   ( 2 )

Passo 4

Para o instante pedido, temos o ângulo de elevação ( θ ) é π / 4 radianos e está crescendo a uma taxa de 0,2   r a d / s . Ou seja,

d θ d t = 0,2   r a d / s

Além disso:

sin ⁡ θ =   sin ⁡ π 4 = 2 2

cos ⁡ θ = cos ⁡ π 4 = 2 2

Passo 5

Agora relacionando todos esses dados com as equações (1) e (2)

d D d t = 1 sin ⁡ θ     d h d t - D cos ⁡ θ d θ d t                         e q u a ç ã o   ( 1 )

d D d t = D ⁡   sin ⁡ θ cos ⁡ θ d θ d t                         e q u a ç ã o   ( 2 )

Substituindo (2) em (1):

D ⁡   sin ⁡ θ cos ⁡ θ d θ d t   = 1 sin ⁡ θ     d h d t - D cos ⁡ θ d θ d t

Colocando todos os dados que encontramos:

D ⁡   sin ⁡ θ cos ⁡ θ d θ d t   = 1 sin ⁡ θ     d h d t - D cos ⁡ θ d θ d t

3000 2 ⁡   1   0,2 = 1 2 2     d h d t - 3000 2 2 2 0,2

Agora partiu fazer essas contas feias:

600 2   = 2     d h d t - 600

600   = d h d t - 600

d h d t = 1200   p é s / s

Como o enunciado pergunta a que taxa estará subindo o foguete, isso é basicamente o d h d t . Então encontramos nossa resposta 😊

Resposta

1200   p é s / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a linearização de f (x) = 2 // ( 1 - x ) + sqrt(1 + x) - 3,1 em x = 0 .
Encontre a linearização de f (x) = sqrt(1 + x) + s e n x - 0,5 em x = 0 .
Podemos obter uma aproximação útil linear da função f ( x ) = 1 / ( 1 + t g x ) em x = 0 combinando as aproximações 1 1 + x ≈ 1 - x e t g x ≈ x para obter 1 1 + t g x ≈ 1 - x Demonstre que esse result
Carretel para cabos Um cabo de televisão é puxado de um grande carretel para ser colocado nos postes telefônicos da rua. Ele é desenrolado do carretel, onde está disposto em camadas de raio constante
Movimento de uma partícula Uma partícula se desloca ao longo da curva y=x 3 / 2 no primeiro quadrante, de modo que sua distância em relação à origem aumenta a uma taxa de 11 unidades por segundo. Dete