Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 - Ex. 55
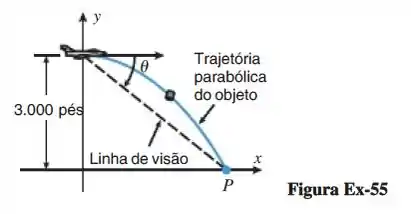
Um avião está voando a uma altura constante de pés acima da água, a uma velocidade de . O piloto deve soltar um pacote de sobrevivência que deve cair na água em um ponto conhecido. Se a resistência do ar for desprezada, então o pacote irá seguir uma trajetória parabólica, cuja equação em relação ao sistema de coordenadas na figura abaixo é:
Onde é a aceleração da gravidade e é a velocidade do avião. Usando , encontre o ângulo da “linha de visão” até o grau mais próximo que resultará no pacote atingindo o alvo.
Passo 1
Fala galera, tudo bem? Olha só, trazendo a imagem da figura:
Vemos que dá pra destacar um triângulo dela:
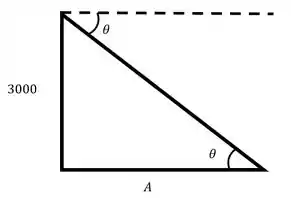
E vamos poder tirar informações de se soubermos pelo menos mais um lado do triângulo! Veja que é o alcance do projétil, e que como:
Quando , a altura, é nula, então , a distância, é ! Sendo assim, vamos ter:
Passo 2
Seja então:
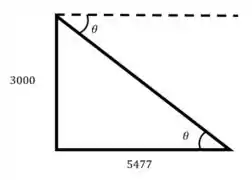
Vemos que:
Então basta a gente fazer a trigonométrica inversa galera! Ó só:
Usando uma famosa ferramenta de planilhas pra calcular esse ângulo, trazemos a função “=ATAN()” pra calcular o arco tangente:
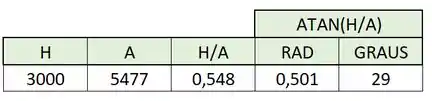
O ângulo que garante então que o pacote vai atingir o alvo é: