Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 - Ex. 54
Uma câmera está posicionada a pés da base de uma rampa de lançamento de mísseis (ver figura a seguir). Se o míssil de comprimento pés for lançado verticalmente, mostre que quando a base do míssil estiver pés acima das lentes da câmera, o ângulo subentendido nas lentes pelo míssil é:x
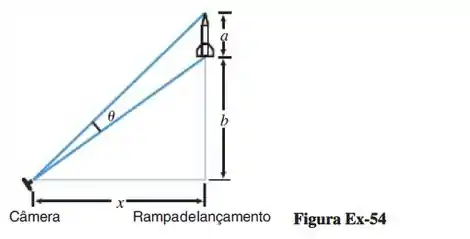
Passo 1
Eita, questão assustadora! Mas calma, vamos lá! Vai dar tudo certo. Pra começar, vou dar mais nomes aos bois. Temos um ângulo, mas que tal estabelecer mais dois?
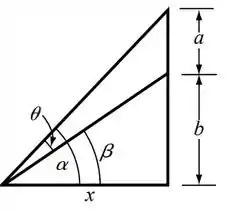
De forma que:
Ok mas pra que isso? Bem, olhando pro triângulo maior, trabalhamos somente com o ângulo e olhando pro triângulo menor, só com o . E achando o valor desses ângulos, achamos !
Passo 2
Então bora lá! Olhando pro triângulo maior, vemos que ele fica assim:
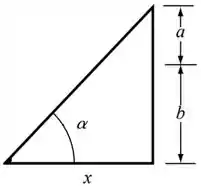
Se conhecemos altura, base e ângulo, temos o suficiente pra achar a tangente!
Invertendo a função, temos:
E logo, fazendo a inversa trigonométrica, encontramos:
Agora, pro triângulo menor, temos:
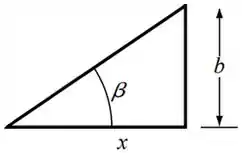
Novamente, temos o suficiente pra achar a tangente!
Invertendo a função, temos:
E logo, fazendo a inversa trigonométrica, encontramos:
Fechamos então galera, como sabemos e , e pela relação do passo :
Temos, de fato, provado que:
Resposta
Provado ao longo da questão