Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.4 - Ex. 24

Um avião está voando horizontalmente a uma altitude constante de 4.000   p é s acima de um ponto de observação fixo (ver figura abaixo). Em um certo instante, o ângulo de elevação θ é de 30 °   e está decrescendo, enquanto a velocidade do avião é de 300   m i l h a s / h .

(a) Com que velocidade estará θ decrescendo naquele instante? Expresse o resultado em graus por segundo.

(b) Com que rapidez estará variando a distância entre o avião e o ponto de observação naquele instante? Expresse o resultado em p é s / s . Use 1   m i l h a   =   5.280   p é s .

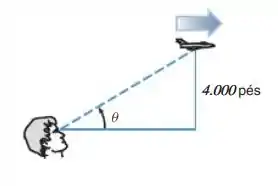
Passo 1

Vamos definir como x a distância do observador até a linha vertical que passa pelo avião, em um instante qualquer. E como D a distância do observador até o avião:

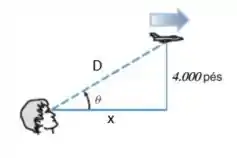
Podemos falar então que:

sin ⁡ θ = 4000 D

cos ⁡ θ = x D

Passo 2

Derivando essas duas expressões teremos:

cos ⁡ θ = x D               ⇒           D cos ⁡ θ = x

d d t ( D cos ⁡ θ ) = d x d t

Pela derivada do produto:

d D d t cos ⁡ θ + D d cos ⁡ θ d t = d x d t

Usando a Regra da Cadeia:

d D d t cos ⁡ θ - D sin ⁡ θ   d θ d t = d x d t                               e q u a ç ã o   ( 1 )

Passo 3

Derivando agora o seno:

sin ⁡ θ = 4000 D                 ⇒           D sin ⁡ θ = 4000

d d t ( D sin ⁡ θ ) = d 4000 d t    

Pela derivada do produto e usando que derivada de constante é zero:

d D d t sin ⁡ θ   + D d sin ⁡ θ d t = 0

Pela regra da cadeia:

d D d t sin ⁡ θ   + D cos ⁡ θ d θ d t = 0                       e q u a ç ã o   ( 2 )

Passo 4

Agora vamos ver os dados que ele dá pra gente:

θ =   30 °   e velocidade do avião de 300   m i l h a s / h , ou seja:

d x d t = 300     m i l h a s h =     1.584.000   p é s h   =   440   p é s / s

Além disso podemos falar que naquele instante

sin ⁡ θ = 1 2 = 4000 D                               ⇒                   D = 8000   p é s

cos ⁡ θ = 3 2

Passo 5

(a)

Relacionando as equações (1) e (2) temos que

d D d t cos ⁡ θ - D sin ⁡ θ   d θ d t = d x d t                               e q u a ç a o   ( 1 )

d D d t sin ⁡ θ   + D cos ⁡ θ d θ d t = 0                                 e q u a ç ã o   ( 2 )

Substituindo (2) em (1):

- 1 sin ⁡ θ D cos ⁡ θ d θ d t cos ⁡ θ - D sin ⁡ θ   d θ d t = d x d t

- ( cos ⁡ θ ) 2   sin ⁡ θ D d θ d t - D sin ⁡ θ   d θ d t = d x d t

Substituindo os dados que encontramos:

- ( 3 2 ) 2   1 2 ( 8000 ) d θ d t - ( 8000 ) 1 2   d θ d t = 440

- 3 2 ( 80 0 ) d θ d t - ( 80 0 ) 1 2   d θ d t = 44

- 3 ( 4 0 0 ) d θ d t - ( 40 0 )   d θ d t = 44

- 16 0 0   d θ d t = 44

d θ d t =   - 11 400     ° / s

Passo 6

(b)

Usando a equação (2):

d D d t sin ⁡ θ   + D cos ⁡ θ d θ d t = 0  

d D d t 1 2 ⁡   + 8000 3 2 - 11 400   = 0  

d D d t 1 2 ⁡ = 800 3 2 11 400    

dD dt ⁡ = 800 ( 3 ) 11 400   = 22 3   p é s / s

Resposta

(a)   - 11 400     ° / s

(b) 22 3   p é s / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sombra de um prédio Em uma manhã, um prédio com 80 pés de altura projeta uma sombra de 60 pés de comprimento. Nesse instante, o ângulo θ que os raios solares projetam no solo aumenta a uma taxa de 0,2
Sombra em movimento Uma luz está acesa no topo de um poste de 50 pés de altura. Uma bola cai da mesma altura em um ponto situado a 30 pés de distância do poste. (Veja a figura a seguir.) A que velocid
Filmagem de um carro em movimento Você está filmando uma corrida a uma distância de 132 pés da pista, seguindo um carro que se desloca a 180 milhas/h (264 pé/s ), como mostra a figura a seguir. Quando
Navios Dois navios a vapor navegam para longe de um ponto O em rotas que formam um ângulo de 120º. O navio A se desloca a 14 nós (milhas náuticas por hora, uma milha náutica equivale a 2.000 jardas).
Débito cardíaco No final de 1860, Adolf Fick, professor de fisiologia da Faculdade de Medicina de Würzberg, na Alemanha, desenvolveu um dos métodos usados até hoje para determinar a quantidade de sang