Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.10 - Ex. 39
Sombra em movimento Uma luz está acesa no topo de um poste de 50 pés de altura. Uma bola cai da mesma altura em um ponto situado a 30 pés de distância do poste. (Veja a figura a seguir.) A que velocidade a sombra da bola se desloca no solo 1/2 s depois? (Considere que, durante a queda, a bola percorreu s = pés em t segundos.)
Passo 1
Como todos sabemos a luz em pequenas distâncias percorre uma linha reta e no instante que a bola encontra-se na mesma altura do poste a sombra da bola encontra-se no infinito. A medida que a bola vai descendo surge um ângulo teta no poste que indica o quanto a sombra esta distante. Até um momento que a sombra encontra-se na bola que é quando toca no chão.
Passo 2
A altura da bola varia de acordo com sua equação de movimento:
O que no tempo de 0.5 s nos dá:
Com essa informação conseguimos calcular a distância da sombra de acordo com os triângulos do desenho a seguir.
Pela proporcionalidade dos triângulos podemos tirar que:
Logo: x=345m
Passo 3
Agora vamos montar um outro triângulo com os valores que variam com o tempo:
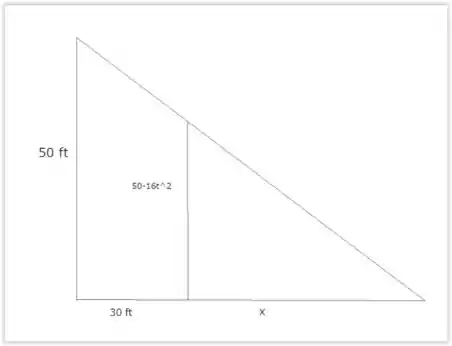
Com esse triângulo podemos fazer a mesma relação de forma mais generalizada:
Fazendo multiplicação cruzada temos:
Cortando os termos iguais e passando negativo para o outro lado ficamos com:
Isolando da equação ficamos com:
Derivando essa equação no tempo temos:
Substituindo agora os valores encontrados no passo anterior:
Encontramos: