Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.4 - Ex. 33

Um farol faz uma revolução a cada 10   s e está localizado em um navio, ancorado a 4   k m de uma praia reta. Com que rapidez o facho de luz do farol estará se movendo ao longo da praia quando fizer com ela um ângulo de 45 ° ?

Passo 1

Vamos entender o que está acontecendo:

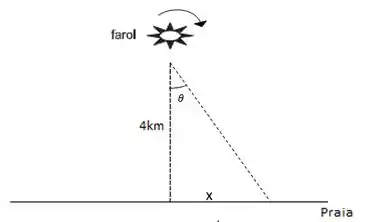
Conforme o farol vai rodando, a luz do farol vai varrendo a praia. Vamos falar que num instante qualquer a distância entre o ponto onde a luz do farol aponta e a reta que liga o farol a praia é x , e o ângulo entre a luz do farol e a mesma reta é θ .

Podemos falar então que:

tan ⁡ θ = x 4

Passo 2

Quando o enunciado diz que o farol faz uma revolução a cada 10   s ,   e uma revolução é uma volta completa, temos que o farol roda 360 ° = 2 π a cada dez segundos. Então por segundo temos que o farol roda:

2 π 10 = π 5   r a d / s

Mas olha que maneiro, isso é justamente a taxa de variação do ângulo θ , ou seja:

d θ d t = π 5 r a d s

Passo 3

Mas já que estamos interessados em saber com que rapidez o facho de luz do farol estará se movendo ao longo da praia, queremos descobrir o d x / d t naquele instante. Para aparecer essa cara vamos derivar a expressão da tangente que tínhamos encontrado:

d d t ( tan ⁡ θ ) = d d t x 4

( tan ⁡ θ ) '   d θ d t     = 1 4   d x d t

( sec ⁡ θ ) 2 d θ d t = 1 4 d x d t

Passo 4

Para aquele instante, θ = 45 ° , então sec ⁡ θ = 2 .

Substituindo esses dados que temos na expressão que encontramos:

( sec ⁡ θ ) 2 d θ d t = 1 4 d x d t

2 2 π 5 = 1 4 d x d t

d x d t = 8 π 5   k m / s

Resposta

8 π 5   k m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Diagonais Se x, y e z são os comprimentos dos lados de uma caixa retangular, o comprimento comum das diagonais da caixa é s = x 2 + y 2 + z 2 . a. Considerando que x, y e z sejam funções deriváveis de
Balão e bicicleta Um balão sobe verticalmente acima de uma estrada plana a uma velocidade constante de 1 pé/s. Quando está 65 pés acima do solo, uma bicicleta que se desloca a uma velocidade constante
Derretimento de uma camada de gelo Uma bola de ferro esférica com 8 pol de diâmetro está coberta por uma camada de gelo de espessura uniforme. Se o gelo derrete a uma taxa de 10 pol3/min, a que taxa a
Policia rodoviária Um helicóptero da polícia rodoviária sobrevoa uma autoestrada plana a 3 milhas do solo a uma velocidade constante de 120 milhas/h. O piloto vê um carro se aproximar e o radar assina
Movimento em um plano As coordenadas de uma partícula em um plano xy são funções deriváveis do instante t com dx/dt = - 1 m/s e dy/dt = - 5 m/s. Qual a taxa de variação da distância entre a partícula