Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.3 - Ex. 58
Um avião está voando a uma velocidade de , a uma altitude de , e passa diretamente sobre uma estação de radar no instante .
- Expresse a distância horizontal de voo como uma função de .
- Expresse a distância entre o avião e a estação de radar como uma função de .
- Use a composição para expressar como uma função de .
Passo 1
Opa, bora lá! O enunciado fala de um avião que voa em uma velocidade de , a uma altitude de quando passa em cima de um radar, e pede pra gente responder a três itens diferentes.
A situação do nosso avião pode ser representada por essa imagem aqui:
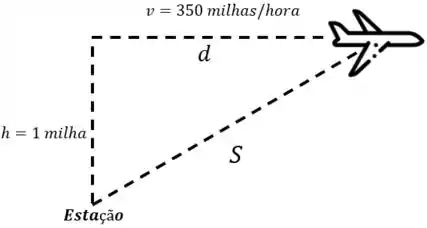
No item a) precisaremos expressar a distância horizontal de voo , desse avião em função do tempo.
Para fazer isso vamos usar a equação horária do espaço, nossa velha conhecida da física, dada por:
No item b) devemos expressar a distância entre o avião e a estação de radar como uma função de . E podemos perceber que essa distância é a hipotenusa do triângulo retângulo formado.
Sendo assim, basta usarmos o teorema de Pitágoras para fazer isso.
Já no item c) pede para que nós usarmos a composição para expressar como uma função de . E para isso, basta juntar o que vamos fazer nos itens a) e b) e deixar em função de .
Vem comigo que vou te ajudar em cada um desses passos
Passo 2
A primeira coisa que precisamos fazer é encontrar uma função da distância em função de . Vamos pensar na primeira função a partir do que foi informado no enunciado e utilizando a equação horária do espaço velha conhecida nossa da física. Então, teremos:
Onde
Passo 3
Agora na letra (b) queremos a distância entre o avião e a estação de radar como uma função de .
Veja a imagem novamente:
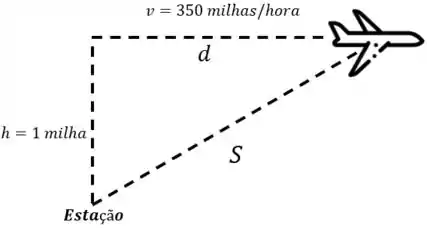
Beleza, ao ganhar distância da estação de radar, essa distância vai ser dada pela hipotenusa que liga a origem até um ponto qualquer. Assim, nossa distância em função de é dada pela seguinte equação:
Então:
Passo 4
Por fim, desejamos expressar a função em função de . Para isso, vamos utilizar a composição de funções fazendo
Prontinho!
Resposta