Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.9 - Ex. 42
Duas carretas, e , estão conectadas por uma corda de que passa por uma polia (veja a figura). O ponto no chão está diretamente abaixo de e entre as carretas. A carreta está sendo puxada, afastando-se de a uma velocidade de . Quão rápido se mova a carreta em direção a no instante em que estiver de ?
Passo 1
O enunciado nos da a seguinte situação:
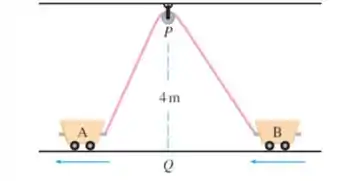
As carretas da figura acima estão conectadas por uma corda de que passa por uma polia . O ponto no chão está diretamente abaixo de e entre as carretas. A carreta está sendo puxada, afastando-se de a uma velocidade de .
Fazendo um desenho esquemático:
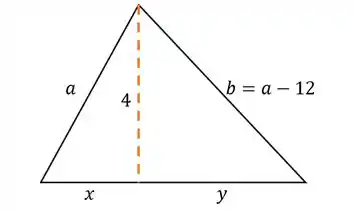
Temos então:
Dito isso, queremos saber: Qual é a taxa de movimento, ou seja, a velocidade, da carreta B em direção ao ponto Q no exato instante em que a carreta A se encontra a uma distância de 3 metros em relação ao ponto Q?
Ou seja, queremos:
Passo 2
Agora a gente precisa escrever equações que relacionam essas vari��veis!
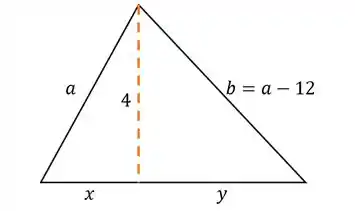
Repara que é como se a gente tivesse dois triângulos retângulos colados, então aplicando pitágora, temos:
Passo 3
Isolando nas duas equações já que ele não nos interessa:
Igualando as duas equações temos:
Passo 4
Agora que temos a relação entre e , vamos derivar relação ao tempo , em segundos. Usando derivação implícita:
Usando a regra da cadeia, temos:
Passo 5
Agora precisamos calcular . Quando estiver de ou seja, :
Como se afasta a , então essa é a taxa de variação com que cresce, ou seja, . No dado instante e . Vamos substituir isso na derivada:
Logo, a distância da carreta ao ponto nesse instante diminui (ele está se aproximando) a uma velocidade de aproximadamente .
Resposta
A distância da carreta ao ponto nesse instante diminui a uma velocidade de aproximadamente .