Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.5 - Ex. 17
Para a barra no Problema 12:
- Faça o gráfico de u em função de x para t = 5, 10, 20, 40, 100 e 200.
- Para cada valor de t usado no item (a), estime o valor de x para o qual a temperatura é a
- Faça o gráfico de u em função de t para x = 10, 20 e 30.
- Desenhe o gráfico tridimensional de u em função de x e de t.
- Quanto tempo vai levar para a barra inteira esfriar e ficar a uma temperatura menor ou igual a 1°C?
maior de todas. Faça o gráfico desses valores em função de t para ver como a posição do ponto
mais quente na barra muda com o tempo.
Passo 1
A solução do problema 12 é:
Fazendo com o t=5,10,20,40,100,200:
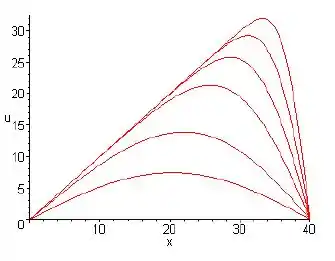
Passo 2
Na letra b:
Analisando os gráficos, temos:
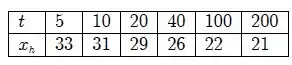
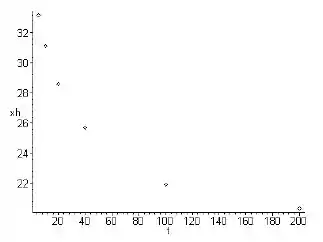
Passo 3
Na letra c:
Fazendo x=5,10,15,20:
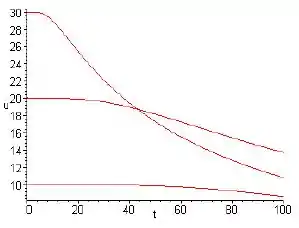
Passo 4
Na letra d:
O gráfico de superfície de :
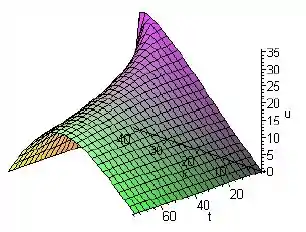
Passo 5
Na letra e:
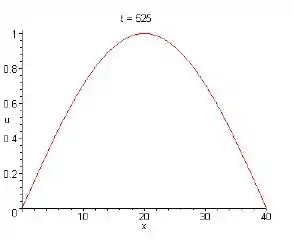
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
A equação do calor em duas dimensões espaciais é: α 2 ( u x x + u y y ) = u t Supondo que u ( x , y , t ) = X ( x ) Y ( y ) T ( t ) , encontre as equações diferenciais ordinárias satisfeitas por X ( x
A equação do calor em duas dimensões espaciais pode ser expressa, em coordenadas polares,na forma α 2 [ u r r + ( 1 r ) u r + ( 1 r 2 ) u θ θ ] = u t Supondo que u ( r , θ , t ) = R ( r ) Θ ( θ ) T (
Para a barra do Problema 18, encontre o tempo necessário para o centro da barra esfriar a umatemperatura de 5°C se a barra for feita de (a) prata, (b) alumínio, (c) ferro fundido.
Siga as instruções no Problema 14 para a barra no Problema 10.