Exercícios de Equação do Calor – Homogênea - Lista de Exercícios Resolvida
Questão 2
Usando separação de variáveis, encontrar a solução da seguinte equação do calor. Explique detalhadamente como se resolve o problema
onde é definida como a extensão par e periódica de período da função onde e esboce o gráfico no intervalo .
Ver solução completaQuestão 3
Dado que
e solução da equação do calor
Determine a solução do problema de valor inicial e de contorno
Ver solução completaQuestão 4
Apresente a extensão par da função
e esboce o gráfico no intervalo .
Encontre a série de Fourier da função acima e esboce o gráfico da série de Fourier no intervalo . (Sugestão: Use o Teorema de Convergência de Fourier)
Usando separação de variáveis encontrar a solução da seguinte equação do calor. Explique detalhadamente como se resolve o problema
onde está definida no item .
Ver solução completaQuestão 5
Resolva o seguinte problema de valor de contorno usando o método de separação de variáveis justificando cada passo detalhadamente:
Ver solução completaQuestão 8
Encontre a solução estado estacionário da equação do calor que satisfaz as condições de contorno:
Escolha uma opção:
a)
b)
c)
d)
e)
Ver solução completaQuestão 9
Considere as equações diferenciais de calor numa barra de tamanho dadas a seguir:
Podemos dizer que a solução que melhor representa é dada por:
Escolha uma opção:
a)
b)
c)
d)
Ver solução completaQuestão 11
Responda verdadeiro (V) ou falso (F) para as seguintes questões, justificando-as:
(a) (1pt) Se e são soluções da EDO , então também o é;
(b) (1pt) As funções são soluções da equação de calor;
(c) (1pt) A EDO é linear de ordem 3;
Ver solução completaQuestão 13
Resolva o seguinte problema de condução do calor usando o método de separação de variáveis justificando detalhadamente toda a análise:
Ver solução completaQuestão 14
A equação seguinte modela um problema do fluxo do calor
Use a separação de variáveis para mostrar que a solução desse problema é
Dica: . Estude apenas o caso .
Ver solução completaQuestão 15
Resolva o seguinte problema de condução do calor usando o método de separação de variáveis justificando detalhadamente toda a análise:
Ver solução completaQuestão 16
Resolva o seguinte problema de condução do calor usando o método de separação de variáveis justificando detalhadamente toda a análise:
Ver solução completaQuestão 19
Dado o problema de condução de calor de uma barra metálica,
- Use o método de separação de variáveis para encontrar a solução desse problema.
- Determine a distribuição de temperaturas da barra se a distribuição inicial de calor é dada por:
Questão 20
Use o método da separação de variáveis para resolver o seguinte problema de condução de calor em uma barra metálica:
Ver solução completaQuestão 21
Seja o problema de condução do calor de uma barra metálica,
- Encontre as soluções do problema de valores de contorno associado, problema de Sturm-Liouville. Justifique
- Encontre um conjunto de soluções do problema dado e formule a solução geral
- Qual será a temperatura em cada ponto da barra se tiver uma distribuição inicial de calor dada por:
Questão 22
Dada a seguinte equação do calor:
- O método de seperação de variáveis supõe que a solução da equação do calor é . Usando esse método mostre como se chega ao sistema abaixo onde é a constante de separação. Analise os casos , e .
- Substituindo os valores , e escolha a extensão par ou ímpar de período que resolve o problema em (a) encontrando a solução . Especifique os coeficientes dessa solução SEM calcular a integral.
Questão 23
Dada a seguinte equação do calor:
- O método de seperação de variáveis supõe que a solução da equação do calor é . Usando esse método mostre como se chega ao sistema abaixo onde é a constante de separação. Analise os casos , e .
- Substituindo os valores , e escolha a extensão par ou ímpar de período que resolve o problema em (a) encontrando a solução . Especifique os coeficientes dessa solução SEM calcular a integral.
Questão 24
- Apresente num gráfico a extensão ímpar e periódica de período da função
- Encontre a série de Fourier.
- Usando o método de separação de variáveis, encontrar a solução da seguinte equação de calor. Explique detalhadamente como se resolve o problema.
Onde é a função descrita no item (a).
Ver solução completaQuestão 25
Determine a extensão ímpar periódica de período da função para esboçando o gráfico no intervalo
Encontre a série de Fourier de senos da extensão ímpar periódica da função para
Resolva o seguinte problema de valor de contorno usando o método de separação de variáveis justificando cada passo detalhadamente:
Ver solução completaQuestão 27
Dado que
e solução da equação do calor
Determine a solução do problema de valor inicial e de contorno
Ver solução completaQuestão 28
Use o método da separação de variáveis para resolver o seguinte problema de condução de calor em uma barra metálica:
Ver solução completaQuestão 29
Questão 4: Utilize o método de Separação de Variáveis para encontrar a solução do problema
Ver solução completaQuestão 30
Questão 4: Considere a EDP do calor, sendo :
Onde está descrita no item a seguir:
- Mostre a função , como sendo a extensão ímpar e periódica de período da função , que está definida em e esboce seu gráfico no interior de , usando o fato de que , com .
- Calcule a série de Fourier da função dada no item .
- Usando os resultados dos itens e , calcule (mostrando os detalhes) a EDP do problema acima usando o método de separação de variáveis.
Questão 31
Questão 2: Resolva o problema de condução de calor em uma barra metálica:
Ver solução completaQuestão 32
Apresente a extensão par e periódica de período da função onde e esboce o gráfico no intervalo .
Encontre a série de Fourier da função acima.
Usando separação de variáveis, encontrar a solução da seguinte equação do calor. Explique detalhadamente como se resolve o problema
onde é a função definida no item .
Ver solução completaQuestão 33
Resolva o seguinte problema de valor de contorno usando o método de separação de variáveis justificando detalhadamente toda a análise:
Ver solução completaQuestão 34
Encontre a solução estado estacionário da equação do calor que satisfaz as condições de contorno:
Escolha uma opção:
a)
b)
c)
d)
e)
Ver solução completaQuestão 36
Resolva o problema do fluxo do calor com fonte de calor externo dado por
Dicas: A solução é dada por . Para achar , resolva o PVI
Já onde os são determinados pela expansão em série de Fourier dos senos de . Use que é se e é se . Use direto que .
Ver solução completaQuestão 37
Resolva o problema de condução de calor em uma barra de comprimento metro e com extremidades isoladas:
Ver solução completaQuestão 38
Questão 2: Considere uma barra uniforme de comprimento para a qual a uma temperatura inicial dada por , com as extremidades mantidas a temperatura . Determine a distribuição de temperaturas da barra.
Ver solução completaQuestão 40
Resolva o seguinte problema do fluxo do calor
Onde
Dica: Avalie os coeficientes da série de Fourier dos senos no caso em que for par e for ímpar.
Ver solução completaQuestão 41
Use o método de separação de variáveis para resolver o seguinte problema de condução de calor em barra metálica:
Ver solução completaQuestão 42
Resolva o seguinte problema de valor de contorno usando o método de separação de variáveis justificando detalhadamente TODA a análise
Ver solução completaQuestão 43
Considere a função periódica de período , que no intervalo é definida por
- Determine os coeficientes de Fourier de .
- Use o teorema de Fourier para calcular a soma da série,
- Resolva o problema de condução de calor:
Questão 44
Considere o problema de condução de calor:
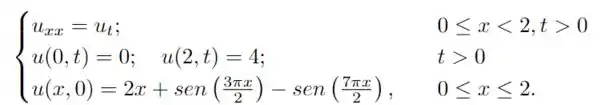
Encontre a solução estacionária do problema.
Ver solução completaQuestão 45
Determine a solução do problema de condução do calor
A solução obtida satisfaz a condição inicial?
Ver solução completaQuestão 46
Suponha que os extremos esquerdo e direito de uma barra homogênea são introduzidos em recipientes com líquidos a temperatura e , respectivamente. Utilizando a Lei de Resfriamento de Newton é possível deduzir que a densidade de fluxo de calor através das extremidades, deve satisfazer as igualdades:
onde e são constantes positivas que representam a condutividade térmica do material da barra e o coeficiente de transferência de calor, respectivamente entre o líquido e os extremos da barra.
Suponha que e são nulas, ou seja, ambos os líquidos estão sendo mantidos a temperatura zero.
a) Escreva o problema de valor inicial com condições de fronteira para a equação do calor que corresponda com a situação física descrita acima.
Ver solução completa