Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.5 - Ex. 15
Siga as instruções no Problema 14 para a barra no Problema 10.
Passo 1
No problema 10 nós temos:
Então, na letra a:
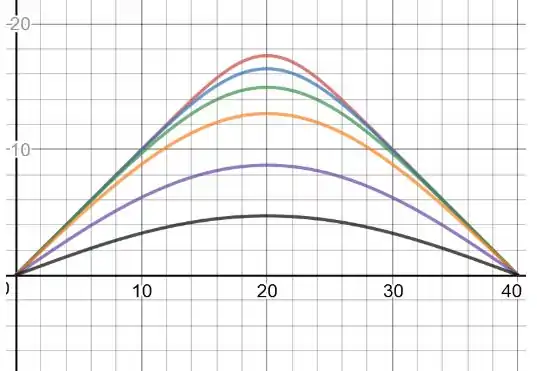
Passo 2
Letra b:
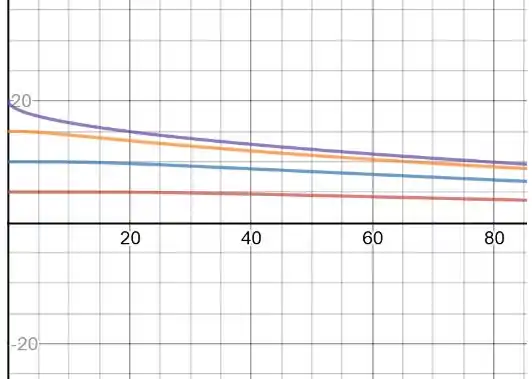
Passo 3
Na letra c:
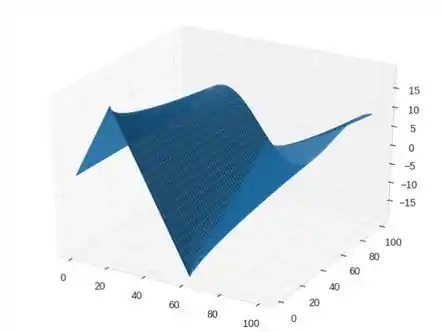
Passo 4
Na letra d:
Podemos brincar com os valores de t para descobrir que para 451.59 o máximo está em 1.0001 e para 451.60 o máximo não é maior que 1.
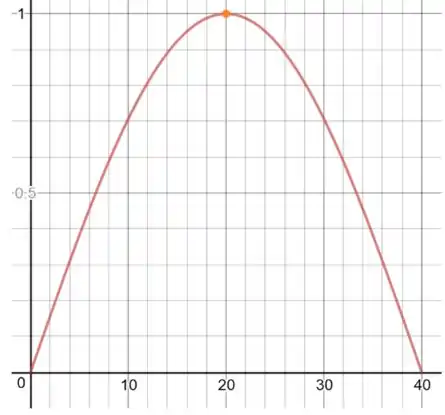
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Para a barra no Problema 19: Faça o gráfico de u em função de x para t = 5, 10, 20, 40, 100 e 200. Coloque todos os gráficos no mesmo conjunto de eixos, obtendo, assim, uma visão de como a distribuiçã
Considere a condução de calor em uma barra com 40 cm de comprimento cujas extremidades são mantidas à temperatura 0°C para todo t0. Encontre uma expressão para a temperatura u(x, t) quando a distribui
Encontre a solução do problema de condução de calor 100 u x x = u t ,0x1 ,t0 ; u ( 0 , t ) = 0 ,u ( 1 , t ) = 0 ,t0 ; u ( x , 0 ) = s e n 2 π x - s e n 5 π x ,0 ≤ x ≤ 1
Considere a condução de calor em uma barra com 40 cm de comprimento cujas extremidades sãomantidas à temperatura 0°C para todo t0 . Em cada um dos problemas de 9 a 12, encontre umaexpressão para a tem
Encontre a solução do problema de condução de calor u x x = 4 u t ,0x2 ,t0 ; u ( 0 , t ) = 0 ,u ( 2 , t ) = 0 ,t0 ; u ( x , 0 ) = 2 s i n ( π x 2 ) - s i n π x + 4 s i n 2 π x ,0 ≤ x ≤