Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.5 - Ex. 14
Para a barra no Problema 19:
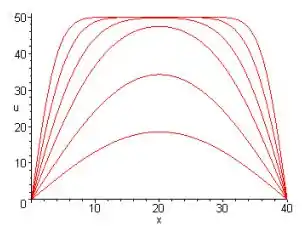
- Faça o gráfico de u em função de x para t = 5, 10, 20, 40, 100 e 200. Coloque todos os gráficos no mesmo conjunto de eixos, obtendo, assim, uma visão de como a distribuição de temperatura varia com o tempo.
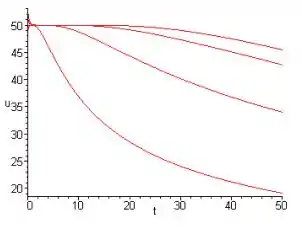
- Faça o gráfico de u em função de t para x = 5, 10, 15, 20. 15. 16. 17. 18. 19. 20. 21.
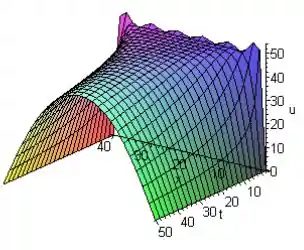
- Desenhe um gráfico tridimensional de u em função de x e de t.
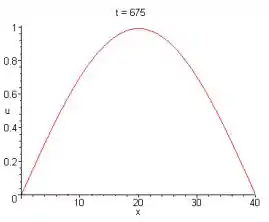
- Quanto tempo vai levar para a barra inteira esfriar e ficar a uma temperatura menor ou igual a 1°C?
Passo 1
Letra a:
A solução do problema de condução de calor fornecido é
Tendo
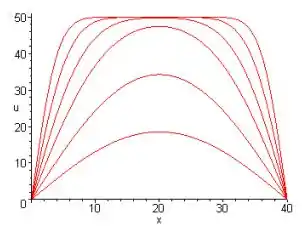
Passo 2
Letra b:
Tendo
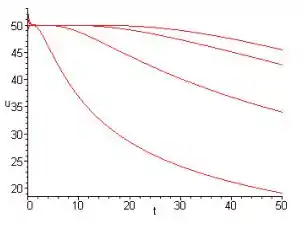
Passo 3
Letra c:
Gráfico da superfície de
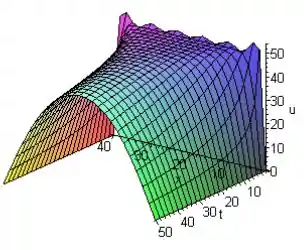
Passo 4
Letra d:
Resposta
Exercícios de Livros Relacionados
A equação do calor em duas dimensões espaciais pode ser expressa, em coordenadas polares,na forma α 2 [ u r r + ( 1 r ) u r + ( 1 r 2 ) u θ θ ] = u t Supondo que u ( r , θ , t ) = R ( r ) Θ ( θ ) T (
Para a barra do Problema 18, encontre o tempo necessário para o centro da barra esfriar a umatemperatura de 5°C se a barra for feita de (a) prata, (b) alumínio, (c) ferro fundido.
Siga as instruções no Problema 14 para a barra no Problema 10.
Para a barra no Problema 12:Faça o gráfico de u em função de x para t = 5, 10, 20, 40, 100 e 200.Para cada valor de t usado no item (a), estime o valor de x para o qual a temperatura é amaior de todas
Em cada um dos problemas de 1 a 6, determine se o método de separação de variáveis pode ser usado para substituir a equação diferencial parcial dada por um par de equações diferenciais ordinárias. Se