Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.5 - Ex. 60
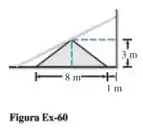
Uma barreira de concreto cuja seção transversal é um triângulo isósceles acompanha um muro a uma distância de metro em um terreno plano. A altura da barreira é de e a base da seção transversal mede . Um cano de diâmetro desprezível apoiado na barreira tem uma ponta no chão e a outra no muro (Figura Ex-60). Qual é o comprimento mínimo que pode ter esse cano?
Passo 1
Então pessoal, a fim de facilitar nossa visualização sobre o problema e também a fim de facilitar nossa visualização sobre os comprimentos que iremos constantemente falar aqui na resolução, vamos esboçar nosso problema em termos dos pontos , se liga:
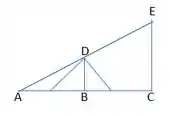
De acordo com o que foi cedido pelo enunciado, temos que:
(escolha nossa)
Por fim:
Show, escrevemos todos os dados que temos!
Passo 2
Se observarmos a figura que desenhamos, veremos que o triângulo retângulo é semelhante ao triângulo retângulo , logo:
E por semelhança de triângulos:
Então:
Substituindo pelos valores que encontramos no passo 1:
Vale ressaltar que essa restrição de se dá porque é o tamanho mínimo (horizontal) que o cano pode ter, de acordo com a figura do enunciado!
Passo 3
Agora que temos uma expressão para o comprimento do cano, devemos encontrar o valor de para que seja mínimo! Aplicando a ideia de máximos e mínimos:
Como , então SEMPRE! Sendo assim, o comprimento mínimo ocorrerá em , pois não podemos admitir valores menores! Substituindo em :
E essa é a nossa resolução, galera! 😉