Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 1.2 - Ex. 16
Um barril em forma cilíndrica, com metros de diâmetro e newtons de peso, flutua na água. O barril se movimenta para cima e para baixo ao longo de uma linha vertical. Usando a figura 1.23(b), determine a equação diferencial para o deslocamento vertical , supondo a origem no eixo vertical na superfície da água quando o barril está em repouso. Use o princípio de Archimedes: o impulso da água no barril é igual ao peso da água deslocada. A densidade da água é . Suponha o sentido positivo para baixo e ignore a resistência da água.
Passo 1
Bom, vamos lá pensar nesse problema. A gente tem um barril dentro da água assim olha:
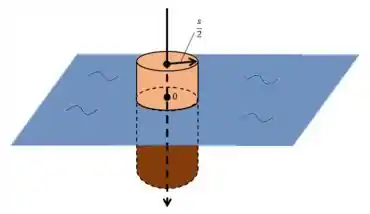
E ele ta flutuando ali na água né, fazendo o movimento pra cima e pra baixo ao longo dessa linha vertical do desenho.
Então podemos pensar em algo assim olha:
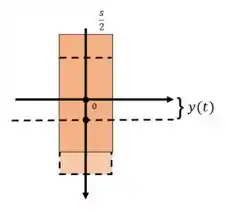
E aí queremos encontrar uma EDO pra esse deslocamento de quando o barril fica indo pra cima e pra baixo, vamos lá?
Passo 2
Pelo princípio de Arquimedes, temos que o impulso da água no barril é igual o peso da água deslocada. Ta, mas qual é o peso da água deslocada?
Gente, o enunciado nos disse que a densidade da água é , podemos usar isso a nosso favor: multiplicando a densidade pelo volume de água deslocada, temos o peso, sacou? Afinal, pensando nas unidades de medida: hihihi
Então:
Mas e aí, qual é o volume de água deslocada? Como o barril é um cilindro, vamos usar o volume de cilindro:
No barril, temos e a altura vai ser justamente o deslocamento (lembrando que não estamos calculando o volume do barril como um todo, e sim o volume de barril que sobe e desce)
Então:
Passo 3
Já encontramos o impulso que a água faz no barril, que é uma força que vai pra cima, certo?
Mas também temos a força peso do barril, que é uma força que aponta para baixo e vale , então, usando a segunda lei de Newton:
Podemos escrever o peso como , sendo que a massa vale :
Mas a aceleração é a segunda derivada da posição, então:
Então, chegamos na nossa equação diferencial: