Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.5 - Ex. 4

Os problemas de 1 a 6 envolvem equações da forma Em cada problema, esboce o gráfico de em função de , determine os pontos críticos (de equilíbrio) e classifique cada um como assintoticamente estável ou instável. Desenhe a reta de fase e esboce diversos gráficos de soluções no plano

Passo 1

4- A função que vamos fazer o gráfico é:

O valor da população inicial está no intervalo , então ele vai ficar:

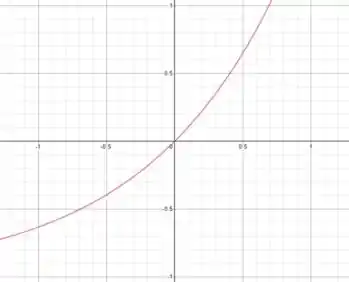
Passo 2

E o esboço das várias soluções é:

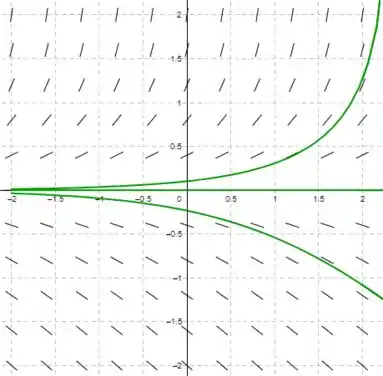
Como dá para ver, o único ponto de equilíbrio é , como as soluções vizinhas divergem desse valor à medida que cresce, isso significa que é uma solução assintoticamente instável.

Passo 3

Com esse gráfico, podemos escrever a reta de fases, como as soluções decrescem para e crescem para , então:

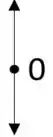
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Pela lei da gravitação universal de Newton, a aceleração de queda livre a de um corpo, tal como o satélite mostrado na Figura 1.16 caindo de uma grande altura, não é a constante g . Em vez disso, a ac

A taxa de decaimento de uma substância radioativa é proporcional à quantidade A ( t ) da substância remanescente no instante t . Determine a equação diferencial para a quantidade A ( t ) .

Suponha um tanque na forma de um cilindro circular reto de raio 2m e altura 10m . O tanque está inicialmente cheio de água, e a água vaza por um orifício circular de raio 1 2 c m no fundo. Use as info

Uma droga é injetada na corrente sanguínea de um paciente a uma taxa constante de r gramas por segundo. Simultaneamente, a droga é removida a uma taxa proporcional à quantidade x ( t ) de droga presen

Um tanque de água tem a forma de um hemisfério com raio 5m . A água vaza por um orifício circular de 1c m no fundo plano. Use as informações do Problema 7 para obter a equação diferencial para a altur