Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.2 - Ex. 12
Resolva o Exercício 11 se o ponto estiver a km de .
Passo 1
Essas questões têm um jeito bem metódico de resolver, saca só:
- Precisamos de uma equação que associe a variável que queremos maximizar e outra variável do problema. Essa é normalmente a parte mais difícil do problema.
- Depois que temos essa função, vamos encontrar a derivada dela e procurar os valores onde ela se iguala a e os valores onde ela não existe.
- A partir do Teorema do Valor Extremo vamos encontrar os máximos e mínimos comparando os valores da função original nos extremos do intervalo e nos pontos onde a derivada é nula ou inexistente.
Passo 2
Vamos utilizar o mesmo princípio do exercício 11 para resolver. Do mesmo jeitinho. Vamos mudar o nosso desenho, já que agora a distância entre é diferente. O nosso mapa vai ficar assim:
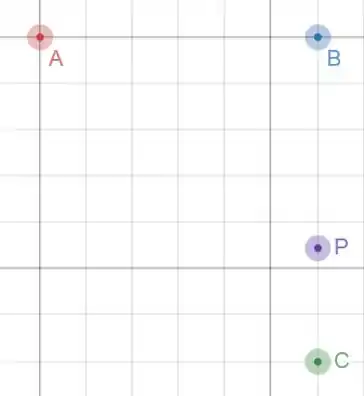
Cada quadradinho representa 1km. Vamos chamar a distância de e tentar encontrar a equação que relaciona o caminho total e o preço de cada transporte. Perceba que temos um triangulo retângulo com um ângulo reto em . Então será a hipotenusa do triangulo e por Pitágoras podemos escrevê-la como:
Mas sabemos que . Então:
Essa é a distância que a mulher andará de barco, para calcular o preço total, ficamos com , já que custa por quilômetro de barco.
Passo 3
Agora vamos para a parte terrestre. A distância que sobra para a mulher andar de carro é o trecho , que podemos escrever como . Já que é a distância total e é o ponto onde ela desceu do barco e vai pegar o carro.
E como custa por quilômetro de carro, o preço na terra fica .
Agora vamos somar os dois preços e teremos a equação do preço total, que é o que queremos!
Agora sim! Podemos derivar a função e encontrar o seu mínimo igualando a sua derivada a ou verificando onde ela não existe.
Passo 4
Derivando :
Repare que a derivada foi a mesma da função do exercício 11.
Perceba que a derivada não existe em . Vamos guardar esse ponto para comparar depois a função original. Igualando a derivada a :
Saca só olhando pro desenho: o pode ser qualquer valor desde até , certo? É o mesmo que dizer que pode ir de até . Então o intervalo fechado que estamos considerando é . Então podemos descartar esse valor que encontramos para a derivada igual a , já que não pertence ao nosso domínio.
Passo 5
Temos 3 pontos para calcular o valor da função: , e ; que são os valores dos limites do intervalo e o valor para o qual a derivada não existe. Vamos calcular para cada um desses valores:
O mais barato então é fazer todo o percurso de barco!
Resposta
O percurso mais barato é fazer todo ele de barco.