Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.4 - Ex. 31
Para o bote do Exercício 30, com que rapidez a corda deve ser puxada se quisermos que o bote se aproxime da doca a uma taxa de , no instante em que restarem de corda?
Passo 1
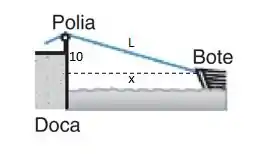
Utilizando a equação encontrada na resolução do Exercício 30, temos que:
Como queremos saber a que rapidez com que a corda deve ser puxada para o bote se aproximar da doca, estamos interessados no
Passo 2
Já que o bote vai se aproximar da doca a uma taxa de , isso nos diz que:
Lembrando que como o bote se aproxima, está diminuindo, por isso o sinal negativo.
Se quisermos usar a equação (1) vamos precisar quanto vale naquele instante. pra saber isso é só a gente usar nosso queridíssimo Pitágoras:
Passo 3
Substituindo todos esses dados na equação (1):
Achamos um , o que faz bastante sentido já que a corda está sendo puxada, ou seja, o está diminuindo 😊