Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.4 - Ex. 30
Um bote é puxado para uma doca por meio de uma corda ligada a uma polia na doca (ver figura abaixo). A corda está ligada à proa do bote em um ponto abaixo da polia. Se a corda for puxada através da polia a uma taxa de , com que taxa o bote estará se aproximando da doca quando restarem de corda?
Passo 1
Vamos começar chamando de a distância do bote até a doca num instante qualquer, e de o comprimento restante de corda.
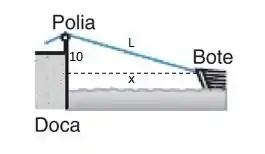
Pelo Teorema de Pitágoras, podemos falar que:
Como queremos saber a que taxa com que o bote estará se aproximando da doca, estamos preocupados em achar basicamente o né?
Então partiu derivar essa expressão em relação ao tempo pro aparecer:
Usando a regra da cadeia e também o fato de derivada de constante ser zero, temos que:
Passo 2
O enunciado nos diz que a corda foi puxada através da polia a uma taxa de . Ou seja, está DIMINUINDO a essa taxa, portanto:
Além disso, naquele instante restam de corda, então
Se quisermos usar a equação (1) vamos precisar quanto vale naquele instante. pra saber isso é só a gente usar nosso queridíssimo Pitágoras:
Passo 3
Substituindo todos esses dados na equação (1):
Achamos um , o que faz bastante sentido já que o barco está se aproximando da doca, ou seja, o está diminuindo 😊