Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.10 - Ex. 29c

Drenagem de um reservatório hemisférico Agua escoa a uma taxa de 6 m 3 /min de um reservatório hemisférico com raio de 13 m, mostrado aqui em perfil.

Responda às questões a seguir, sendo o volume de água em um recipiente hemisférico de raio R dado por V = π 3 y 2 ( 3 R - y ) , quando a água tiver y metros de profundidade.

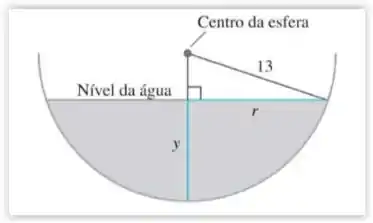
a. Qual será a taxa de variação do nível da água quando a profundidade for de 8 m?

b. Qual será o raio r na superfície da água quando ela tiver y metros de profundidade?

c. Qual será a taxa de variação do raio r quando a profundidade da água for de 8 m?

Passo 1

Com o dado de que a profundidade y vale 8m e com o resultado da letra b e da letra a em mãos podemos deriva-la para poder encontrar a taxa de variação do raio d r d t

r = 26 y - y 2

d y d t = - 0.0133 m m i n

Passo 2

Derivando ela no tempo encontramos:

d r d t = 1 2 1 26 y - y 2 ×   26 d y d t - 2 y d y d t

Passo 3

Substituindo os valores encontramos:

d r d t = 1 2 1 26 × 8 - 8 2 × ( 26 × - 0.0133 - 2 × 8 ×   - 0.0133 )

Fazendo conta encontramos:

d r d t = 1 2 1 12 × ( - 0.133 )

Resposta

d r d t = - 5.542 × 10 - 3   m m i n        

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja l o comprimento da diagonal de um retângulo cujos lados têm comprimentos x e y , e suponha que x e y variem com o tempo. (a) Como estão relacionadas d l d t , d x d t e d y d t ?(b) Se x está cre
Uma escada de 1,3 m está apoiada em uma parede e seu topo desliza sobre a parede para baixo a uma taxa de 0,2 m / s , com que rapidez a base da escada estará se afastando da parede quando o topo estiv
Seja θ (em radianos) um ângulo agudo de um triângulo retâgulo, e sejam x e y , respectivamente, os comprimentos dos lados adjacente e oposto a θ . Suponha, também, que x e y variem com o tempo.(a) Com
Uma quadra de softball é um quadrado cujos lados medem 60p é s é de comprimento. Suponha que um jogador correndo da primeira para a segunda base tenha uma velocidade de 25p é s / s é no instante em qu
Um tanque de água cônico com o vértice para baixo tem um raio de 10m no topo e uma altura de 24m . Se a água fluir dentro do tanque a uma taxa de 20m 3 / m i n , com que velocidade sua profundidade es