4 -
Passo 1
Considere o sistema:
a)
Vamos assumir como a solução do sistema. Portanto iremos substituir esse valor no sistema.
Passo 2
Os valores são as raízes da equação.
Portanto, os autovalores são e .
Passo 3
Quando , a equação fornece,
Cada linha gera a condição:
O autovetor correspondente ao autovalor é:
Passo 4
Para encontrar a segunda solução linearmente independente para o sistema (1), resolva o sistema
Cada linha gera a seguinte equação:
Vamos definir , ou seja, uma constante arbitrária.
Assim, o segundo autovetor correspondente ao autovalor é:
Passo 5
Temos que:
Substitua e na equação acima:
O último termo é um múltiplo de e, portanto, pode ser descartado.
Então, a segunda solução do sistema é:
Passo 6
b)
Assim, a solução geral do sistema (1) é,
Onde e são constantes arbitrárias.
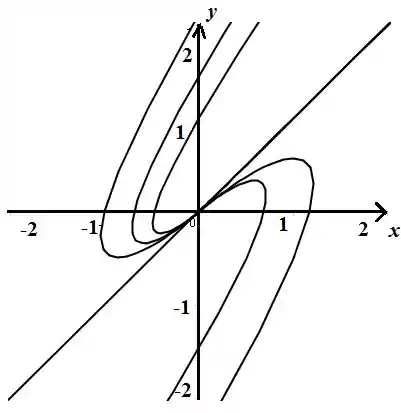
Para valores muito altos de , o termo é dominante, por conta do que está multiplicando. Se observamos bem, quando toda trajetória se aproxima da origem. Da mesma forma para grandes valores negativos de o mesmo termo continua sendo dominante, de mo que . Cada trajetória é assíntota a uma linha paralela a . Portanto, o ponto crítico é um nó assintoticamente estável.
Passo 7
c)
A solução do sistema é:
Portanto, as soluções são:
e
Agora, o esboço das trajetórias é mostrado abaixo:
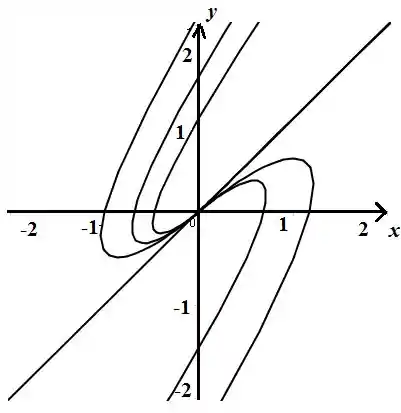
Passo 8
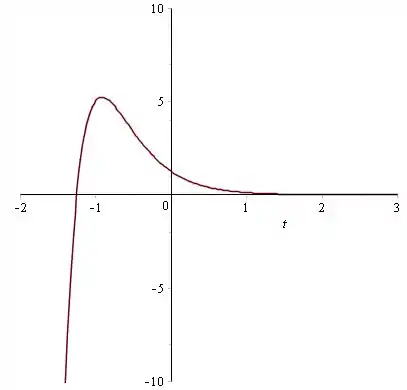
Observe a solução que possui diferentes valores para e :
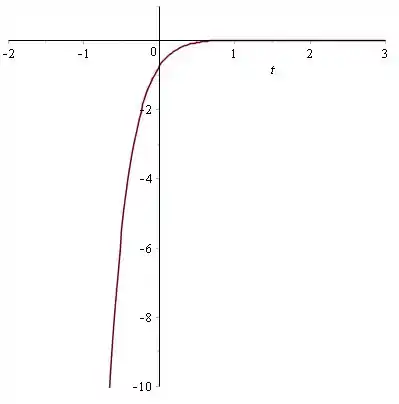
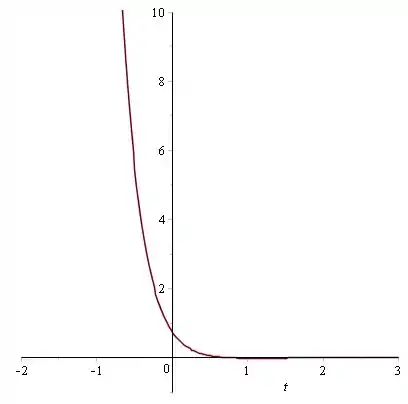
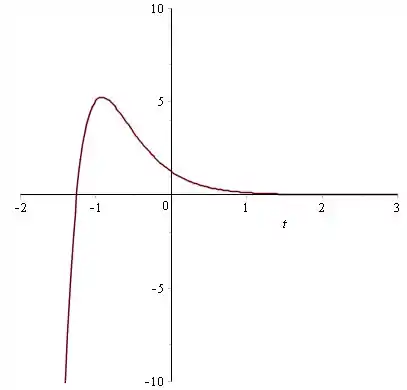
Para ,
Para ,
Para ,
Para ,
Agora vamos esboçar todas essas soluções no plano .
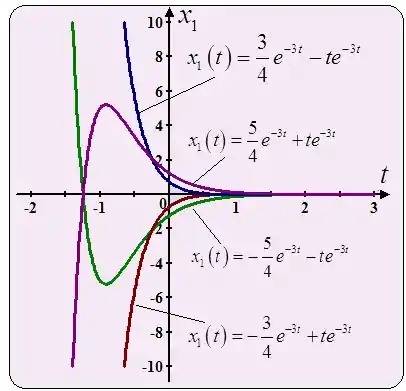
Passo 9
d) Os comandos serão colocados abaixo. Use um software e reproduza para conferir os resultados.
![]()
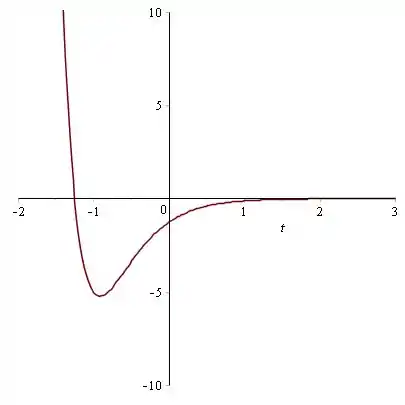
![]()
![]()
![]()
Resposta
- Os autovalores são e .
- O ponto crítico é um nó e estável.
-
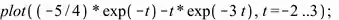
O autovetor correspondente ao autovalor é:
O autovetor correspondente ao autovalor é:
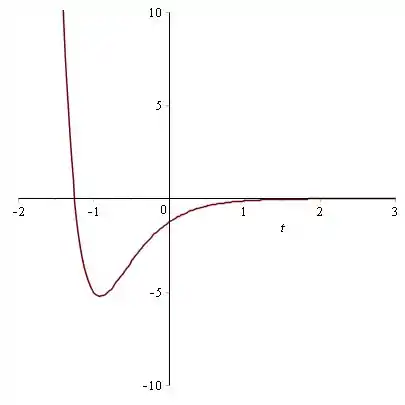
![]()

![]()
![]()