Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.8 - Ex. 5
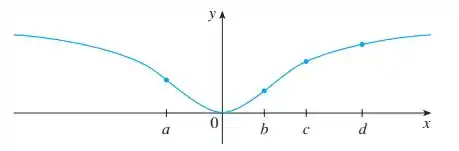
5. Para cada aproximação inicial e, você acha que o método de Newton funcionará e levará à raiz ?
Passo 1
Oi meus queridos...
Nessa questão temos uma curva que é dada e devemos dizer que para as aproximações iniciais , quais delas irão funcionar no método de Newton.
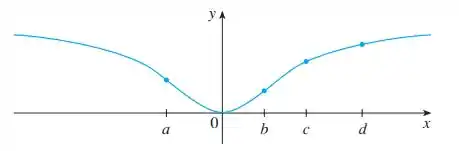
O método de Newton é um método usado para encontrar a raíz de uma função. Para isso, você precisa de um chute inicial e a partir da derivada da função o método te aproxima do ponto onde a função zera.
Geometricamente, o que ele faz a partir da aproximação inicial é caminhar através de uma reta que é dada pela tangente da função naquele ponto e para quando essa reta atinge o eixo .
Por exemplo, em , temos:
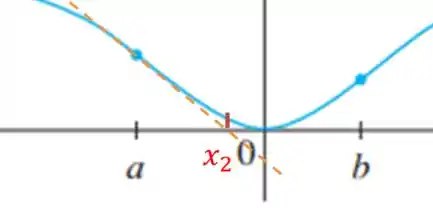
Depois utiliza-se o novo ponto para continuar o processo até chegar-se na raíz.
Passo 2
As aproximações iniciais vão funcionar, pois estará mais próximo da origem, que é onde está a raiz dessa função.
Por exemplo, para temos:
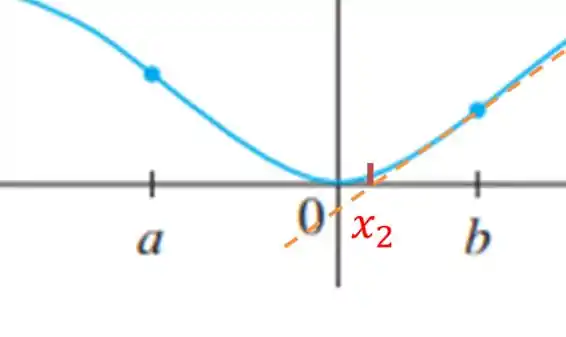
E para temos:
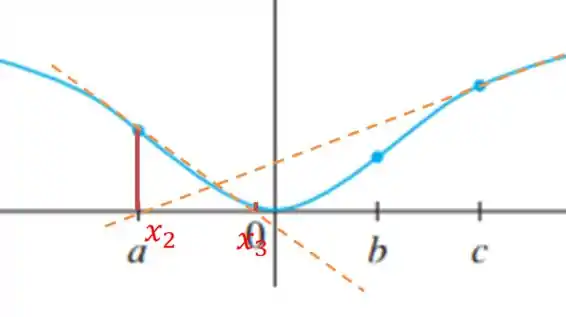
Passo 3
Entretanto para o método não funcionará pois estaremos nos afastando cada vez mais da raiz.
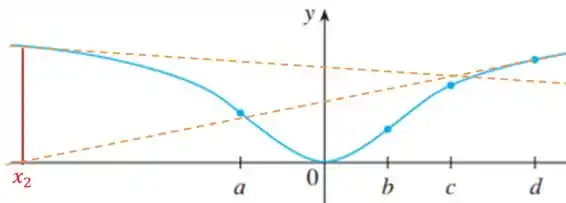
Resposta
O método deve funcionar para
Para , o método não deve funcionar.