Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.3 - Ex. 12
Em cada um dos problemas de 7 a 12:
(a) Esboce o gráfico da função dada.
(b) Expresse em termos da função degrau unitário
Passo 1
O primeiro passo do exercício será esboçar a função com base nas funções por parte dadas.
Montaremos o gráfico analisando o comportamento da função nos intervalos dados. Quando a função é uma constante quando está entre 0 e 2,a função cresce em 2 pontos entre 2 e 5, entre 5 e 7 a funçãose comporta como , em maior que 7 a função decai e se torna constante em 0.
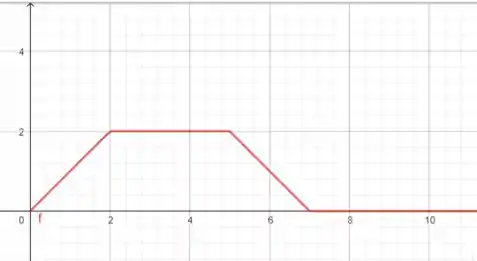
Passo 2
(b) Para descobrir qual é a função envolvida em termos de degrau unitários .
Para isso, vamos das atenção a cada uma das etapas que foram apresentadas nos degraus. Analisando de modo geral:
Foram apresentados intervalos em alguns cenários, onde define-se entre 0 e 2, 2 e 5, 5 e 7, 7. Isso significa que esses pontos extremos dos intervalos, são nossos respectivos .
Então, temos: , e . Isso significa que temos , e
Analisando agora as etapas em si.
Quando recebe o valor de uma constante no intervalo.
Quando aumentamos o intervalo , ela se torna constante em 2 e deixa de ser . Isso acontece quando temos um valor de
No próximo intervalo, a função cresce em 5 pontos, de para . Com
A função cai em uma unidade e zera no último passo, quando
Para zerar:
Então:
Juntando os termos temos: