Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 71

Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar a forma geral do gráfico de f.

71-

y ' = t g 2 θ - 1

- π 2 < θ < π 2

Passo 1

Fazendo y ' = 0 para encontrar os pontos críticos da expressão nós temos:

t g 2 θ - 1 = 0

t g 2 θ = 1

t g   θ = ± 1

Como o intervalo de θ é entre - π 2 e π 2 , logo nós temos os valores iguais a:

θ = - π 4 ;       θ = π 4

Passo 2

Derivando a equação fornecida afim de achar saber se os pontos encontrados são pontos de máximo ou de mínimo e se temos pontos de inflexão:

y ' ' = ( t g 2 θ - 1 ) '

y ' ' = 2 t g   θ × sec 2 ⁡ θ - 0

Passo 3

Testando os pontos críticos temos:

Para θ = - π 4

y ' ' - π 4 = 2 × t g - π 4 × 1 cos 2 ⁡ - π 4 = - 4 → n e g a t i v o

Logo θ = - π 4 é um ponto de máximo local

Para θ = π 4

y ' ' π 4 = 2 × t g π 4 × 1 cos 2 ⁡ π 4 = 4 → p o s i t i v o

Logo para θ = π 4 representa um ponto de mínimo local.

Fazendo agora y ' ' = 0 para saber dos pontos de inflexão temos:

2 t g θ sec 2 ⁡ θ = 0

Como a função secante não pode ser zero, temos que somente a função tangente pode ser zero nessa equação.

t g   θ = 0

Como t g θ = sin ⁡ θ cos ⁡ θ , logo s i n θ = 0 o que ocorre em θ = 0

Logo θ = 0   é um ponto de inflexão

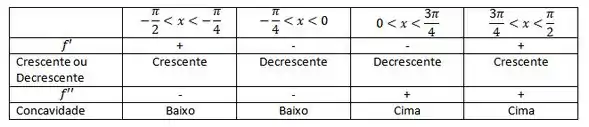
Passo 4

Organizando nossos intervalos:

Resposta

y ' ' = 2 t g   θ × sec 2 ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use ao gráficos dados para estimar o valor de cada dereivada. Esboce então o gráfico de f ' . f ' 0 f ' 1 f ' 2 f ' 3 f ' 4 f ' 5
Use ao gráficos dados para estimar o valor de cada dereivada. Esboce então o gráfico de f ' . f ' - 3 f ' - 2 f ' - 1 f ' 0 f ' 1 f ' 2 f ' 3
Trace ou copie o gráfico da função f dada. (Suponha eixos com a mesma escala.) Use então o método do Exemplo 1 para esboçar o gráfico de f ' .
Trace ou copie o gráfico da função f dada. (Suponha eixos com a mesma escala.) Use então o método do Exemplo 1 para esboçar o gráfico de f ' .
Associe o gráfico de cada função em (a)-(d) com o gráfico de sua derivada em I-IV. Dê razões para suas escolhas.